Упакованные в цилиндрические тубусы чипсы, чтобы они меньше крошились, запекают на жарочных листах, придающих плоским заготовкам форму гиперболического параболоида.
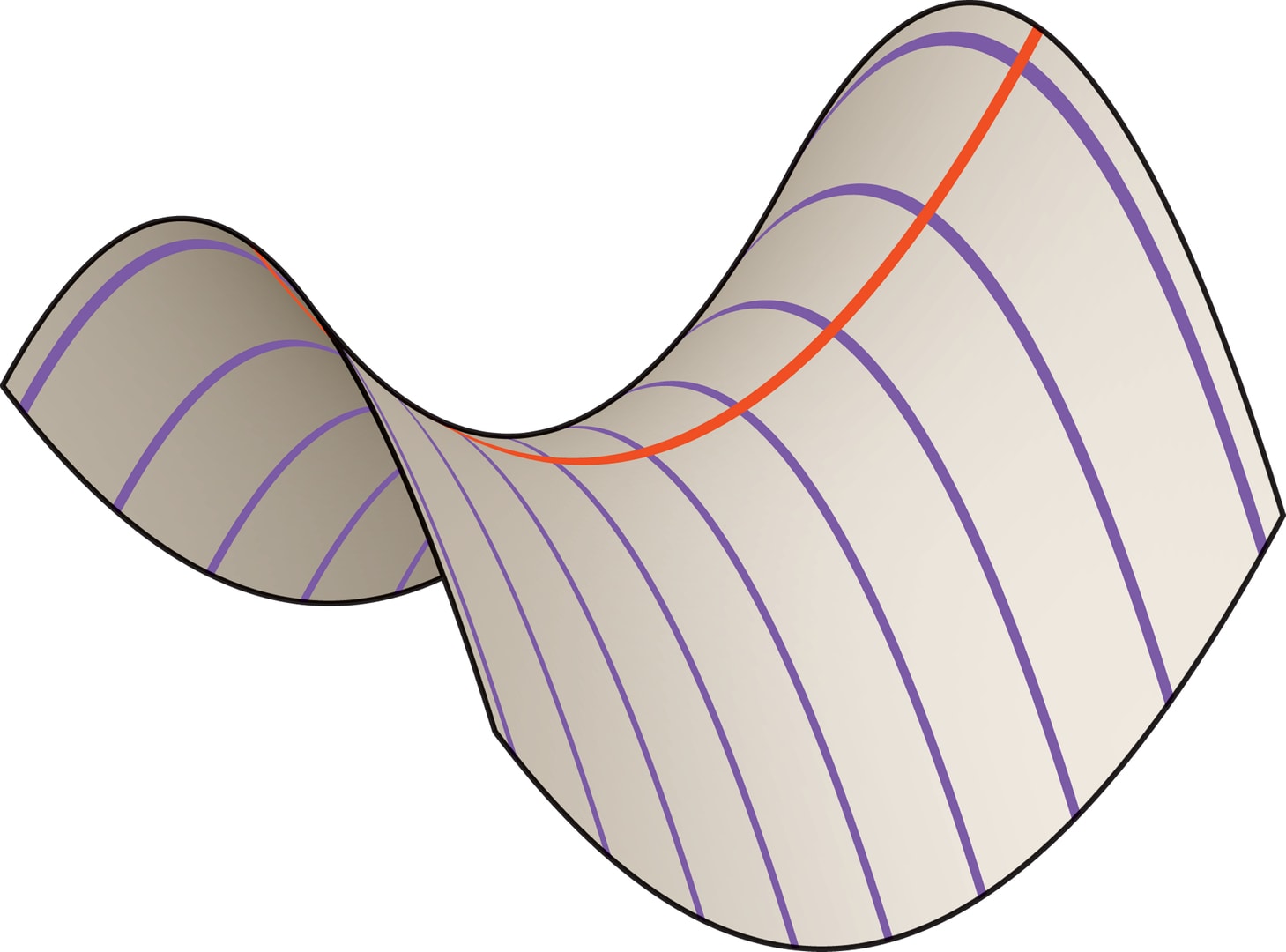
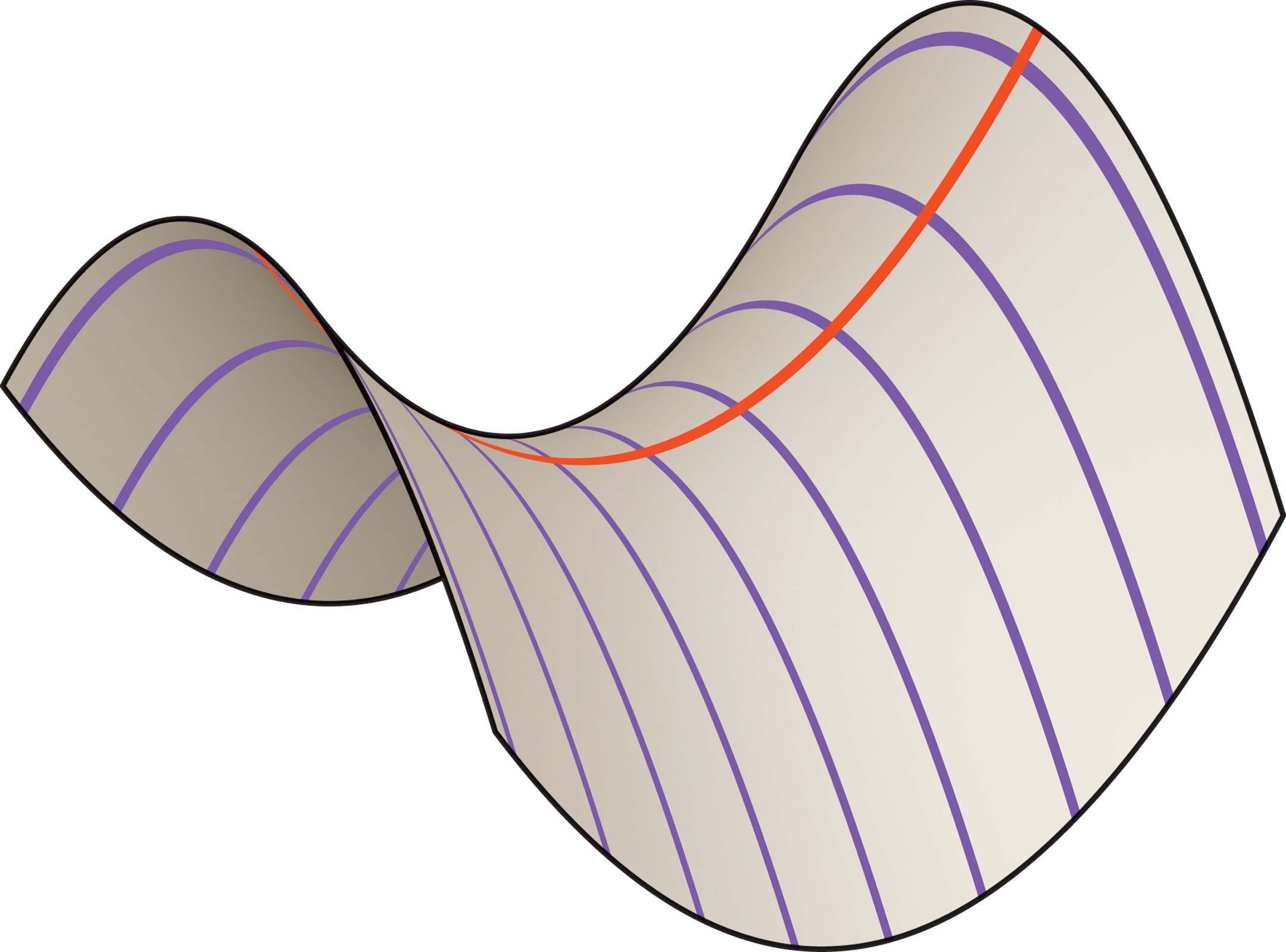
Эта напоминающая седло поверхность образуется при движении параболы (её ветви направлены вниз), вершина которой скользит по другой, неподвижной параболе (ветви направлены вверх). Плоскости парабол в каждый момент времени перпендикулярны, оси — параллельны.
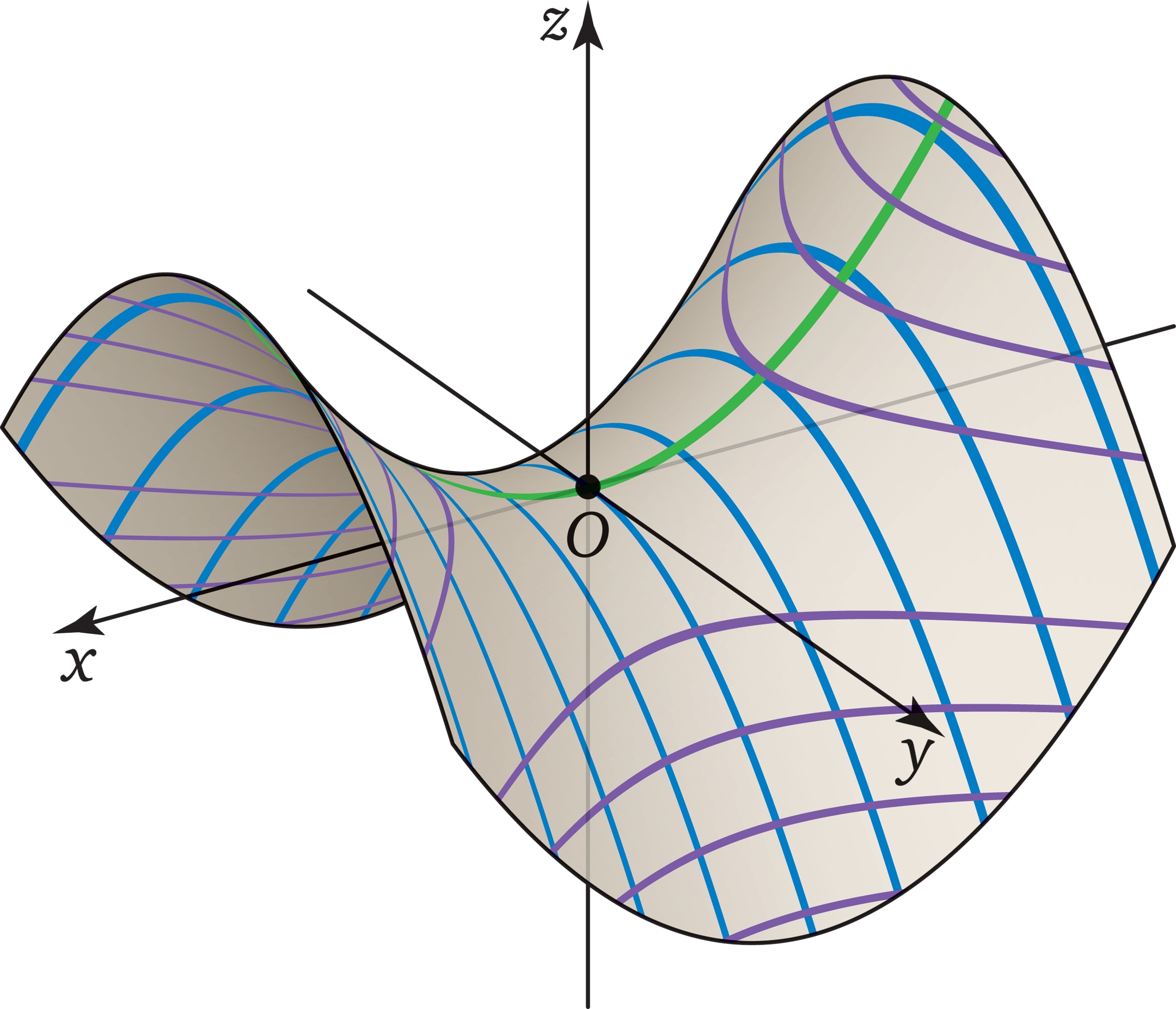
Появление слова «гиперболический» в названии объясняется тем, что при пересечении поверхности с горизонтальной плоскостью получается гипербола. (Если плоскость проходит через центр седла, то гипербола вырождается в пару пересекающихся прямых.)
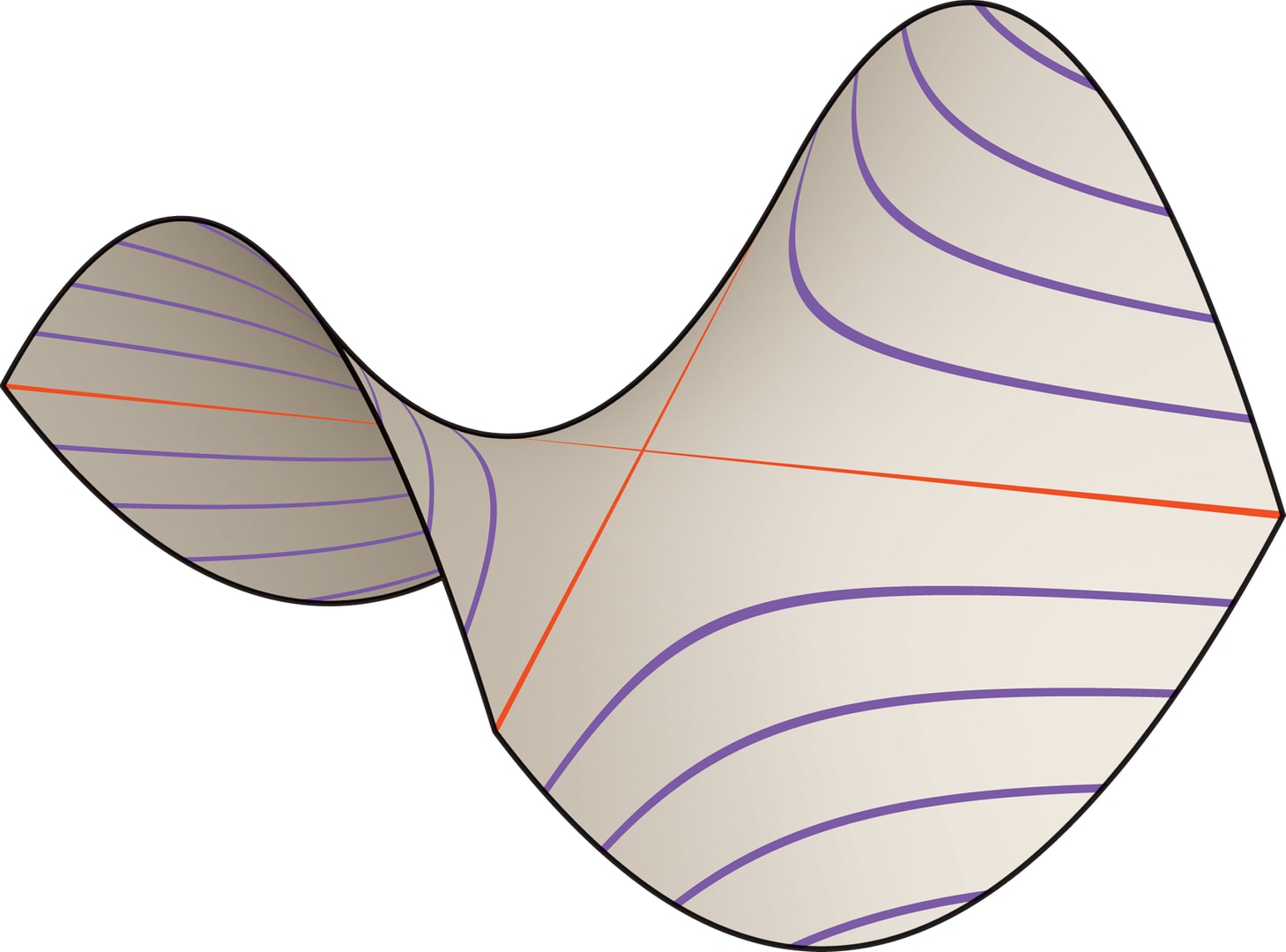
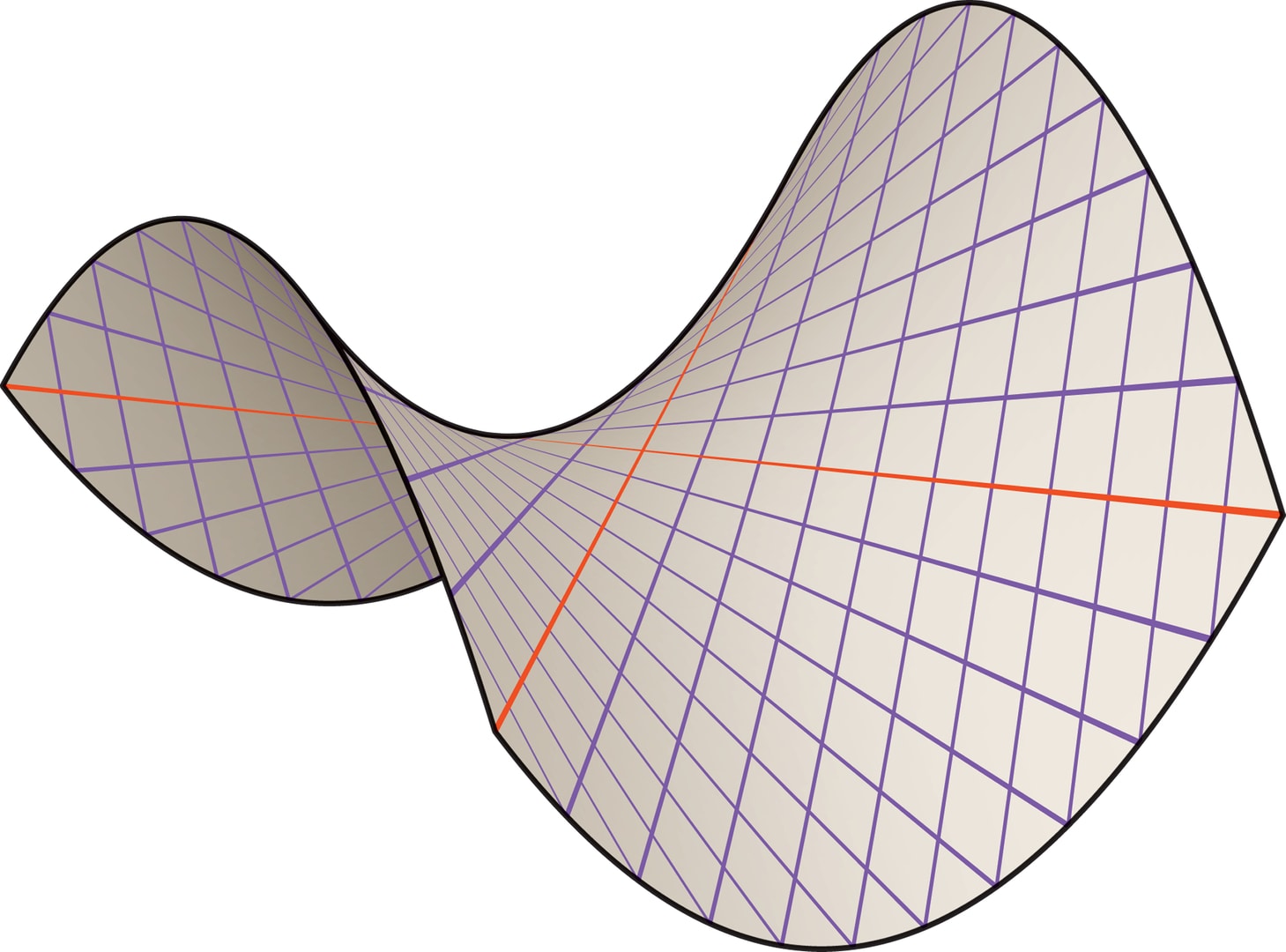
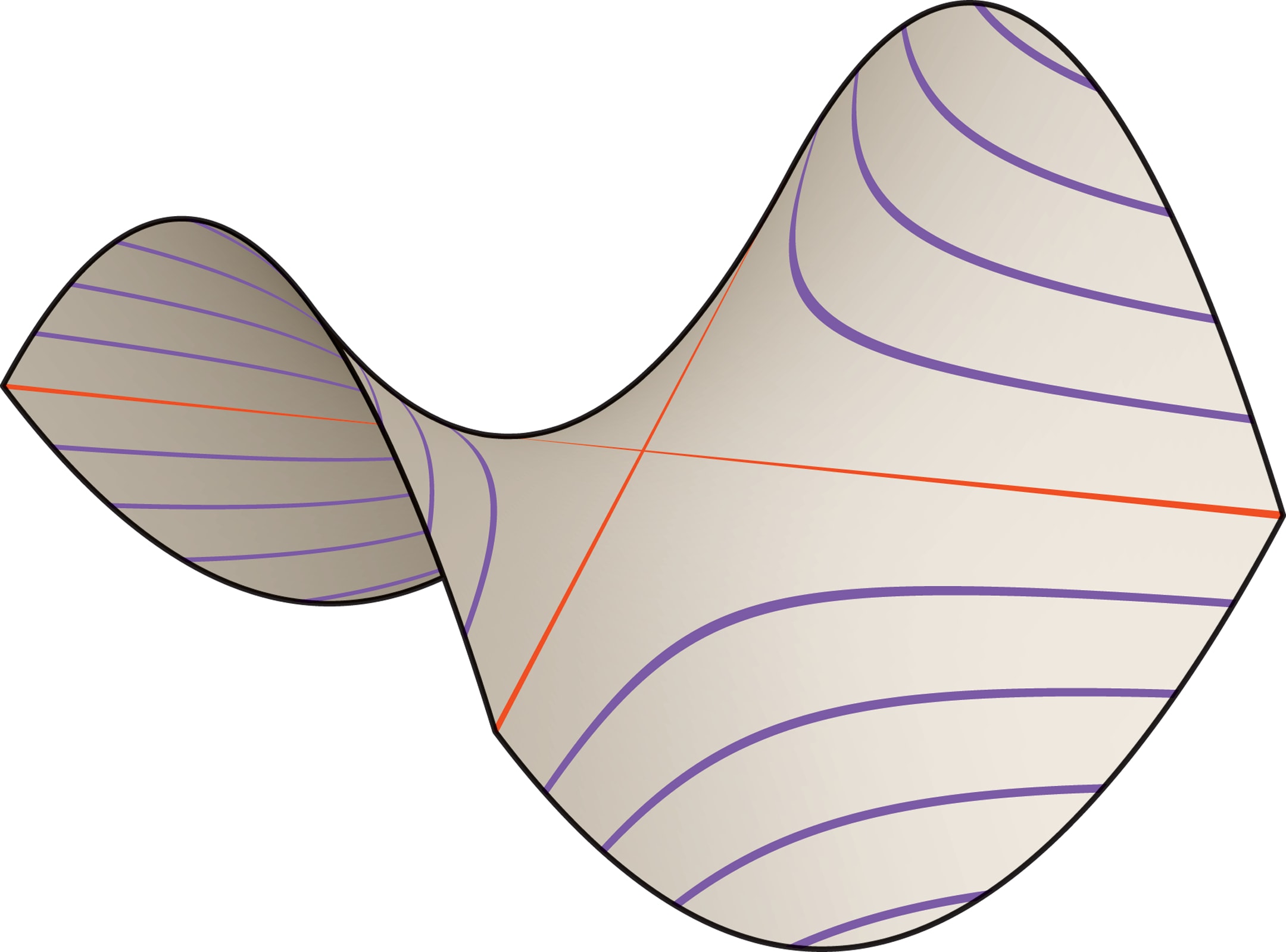
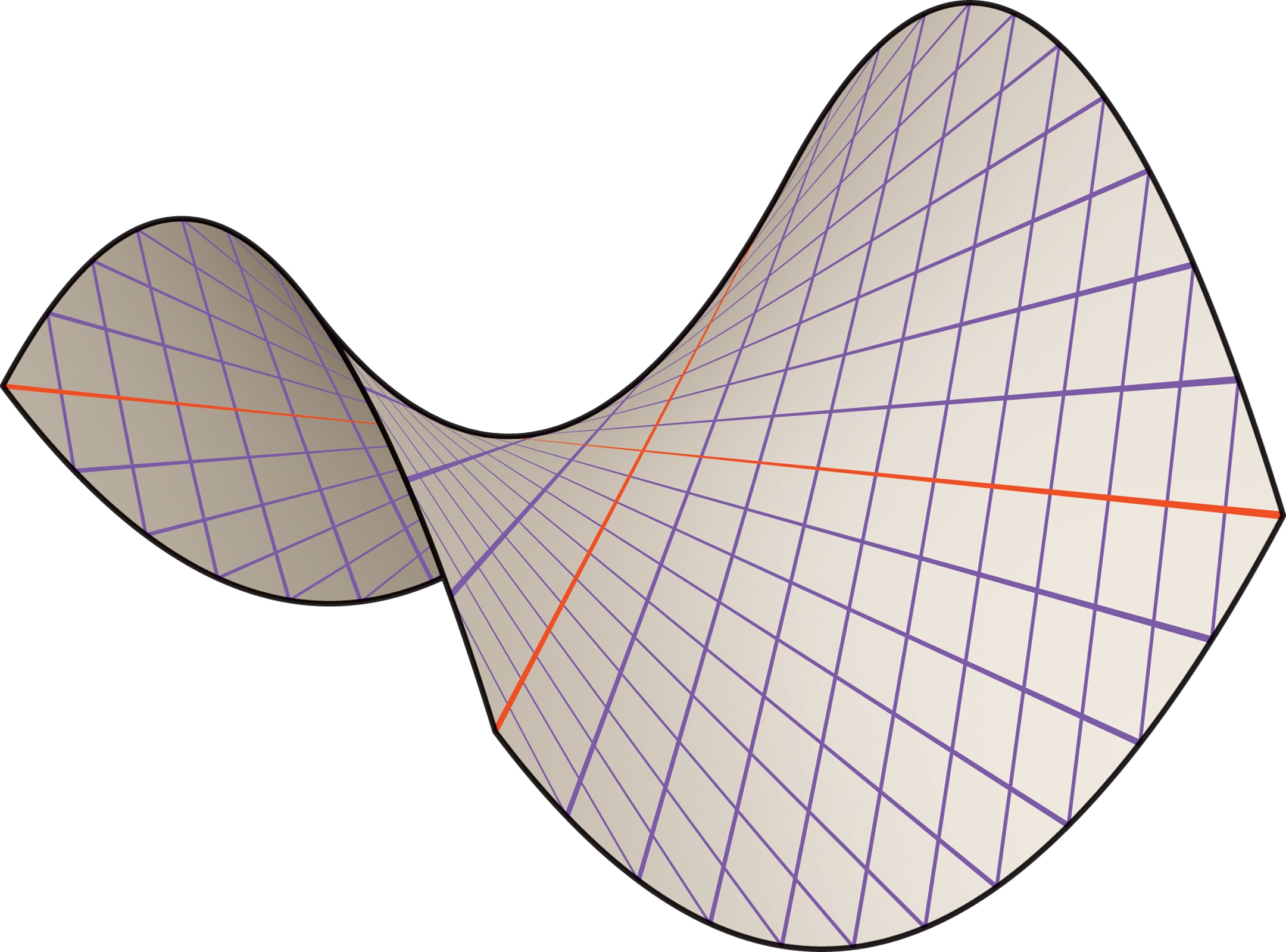
Но кроме парабол и гипербол на гиперболическом параболоиде «живут» и прямые: через каждую точку этой седловидной поверхности проходят две прямые. Каждая из них может двигаться по поверхности гиперболического параболоида, заметая её. В математике поверхности, образованные движением прямой линии (образующей), называются линейчатыми. Простые примеры — цилиндр и конус. А вот линейчатость гиперболического параболоида или однополостного гиперболоида (вспомните конструкции В. Г. Шухова), конечно, удивляет.
Свойство линейчатости проявит себя наглядно, если в крышке тубуса проделать прямолинейную прорезь, а затем взять из стопки чипсов один ломтик и «опустить» его в тубус через полученную щель. Это можно сделать не сломав ломтик, надо только держать (и поворачивать!) его так, чтобы в каждый момент времени через прорезь проходила образующая гиперболического параболоида.
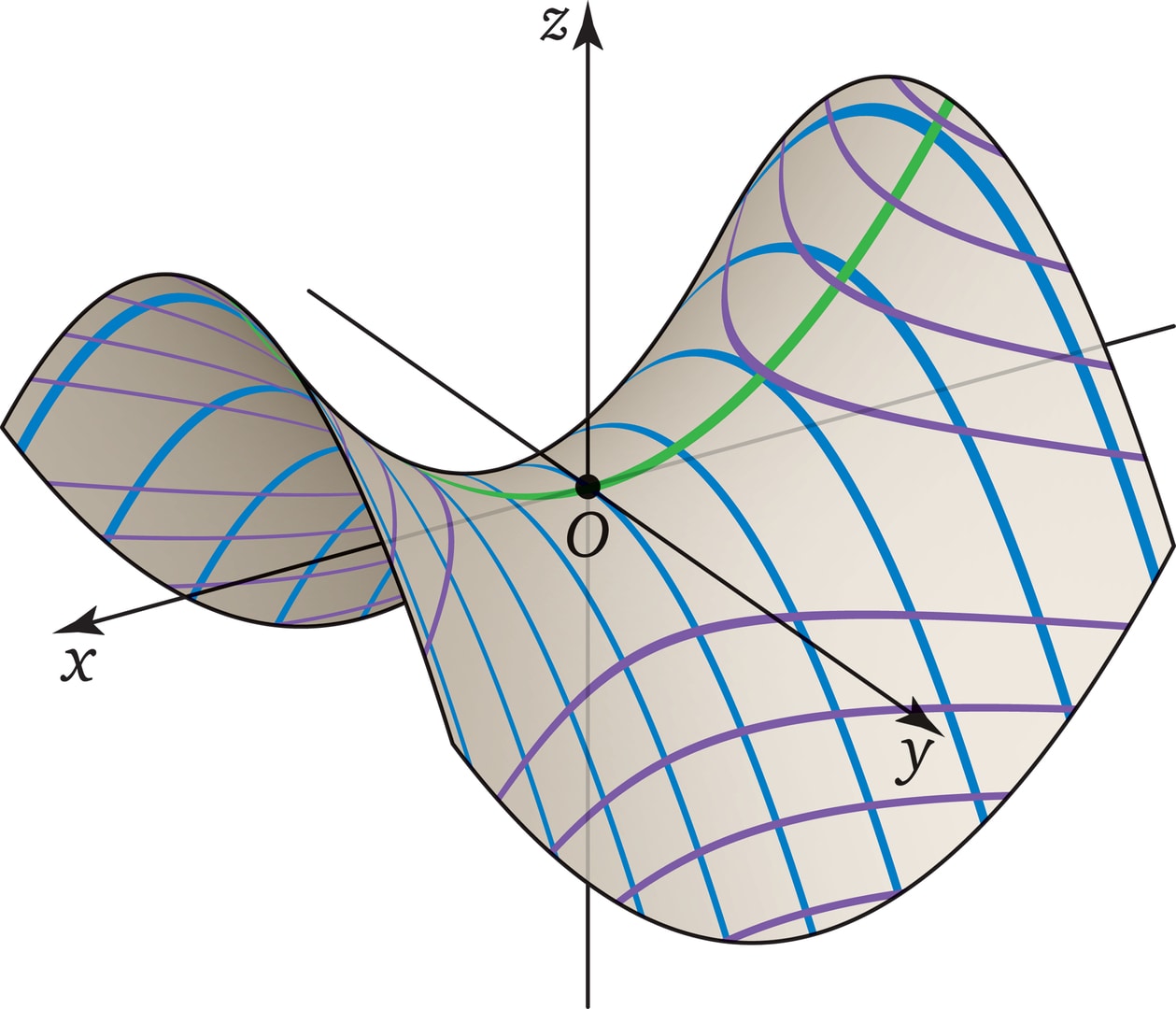
Рассмотрев сечение плоскостью $y=0$, читатель «увидит» неподвижную параболу, а в сечении $x=0$ — параболу, которая скользит вдоль неподвижной. В сечениях плоскостями $z=\mathrm{const}$ ($\ne 0$) получаются гиперболы. Про параболы и гиперболы см. «Параболическая антенна» и «Шуховские башни».
Чипсы: гиперболический параболоид
Седловая поверхность: гиперболический параболоид