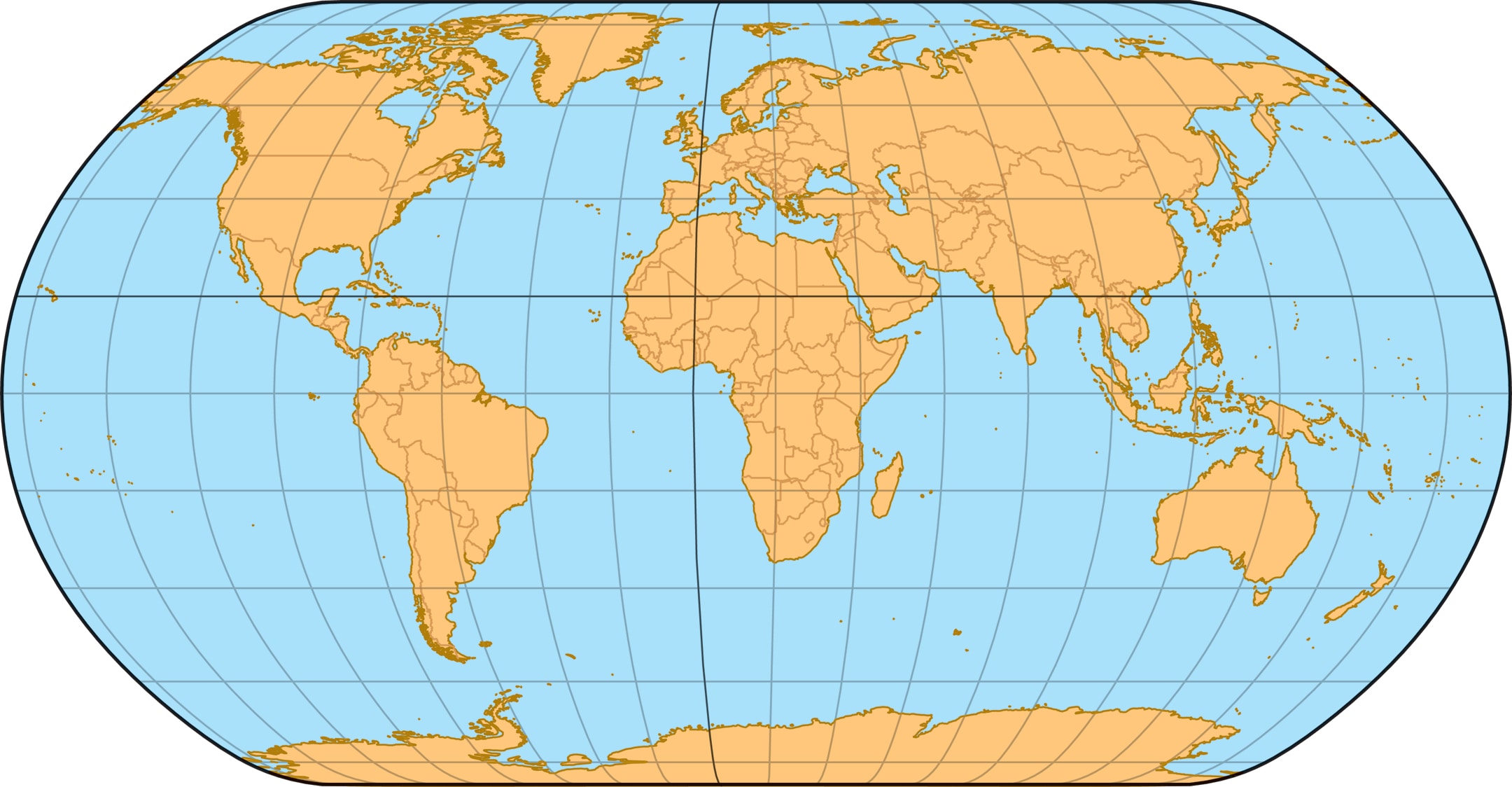
География, буквально «описание Земли», начинается с наглядного представления. Самый популярный способ — географическая карта. Но разглядывание карты может удивить и озадачить. Например, остров Гренландия на некоторых картах занимает больше места, чем вся Южная Америка, хотя его площадь в восемь раз меньше. «Белый континент» Антарктида может предстать и почти круглым пятном, и широкой полосой, занимающей всю нижнюю часть карты Земли. А изображения основной материковой части России могут отличаться настолько, что на одних картах очертания Чукотки визуально находятся на одном уровне с контурами полуострова Таймыр, на других — могут быть выше или ниже. На самом деле именно на Таймыре находится северная оконечность материковой России — мыс Челюскин. Чтобы научиться «читать» географические карты, стоит познакомиться с методами их создания.
Форма Земли достаточно сложна (её название — геоид), но близка к эллипсоиду вращения с полуосями 6378 км и 6357 км: «несферичность» её настольной копии была бы миллиметровой. Наилучший «портрет» Земли — глобус: проекция поверхности Земли на сферу.
Естественная система координат на глобусе (и на Земле) — сферическая, положение точки определяется двумя углами. Долгота отсчитывается от нулевого (Гринвичского) меридиана, широта — от экватора. На глобусе эту систему координат представляет сетка — параллели и меридианы с фиксированным угловым шагом (обычно $10°$—$20°$).
Наглядно-понятный глобус обладает и неустранимыми недостатками: например, невозможно изготовить глобус, на котором детально представлена какая-то местность или город. Получить правильное и удобное изображение земной поверхности на плоской карте — основная задача картографии. Математическая постановка: найти отображение сферы (глобуса) на плоскость (карту), вывести формулы, связывающие координаты точек на глобусе и на карте.
Этой задачей и близкими вопросами геодезии занимались многие великие математики, соединявшие изучение оригинальной математической проблемы с разработкой ценных практических инструментов. Леонард Эйлер писал теоретические работы, а ещё лично чертил и редактировал карты, руководил картографическими работами в Академии наук и гордился тем, что способствовал приведению российской географии «в исправнейшее состояние». К. Ф. Гаусс не только открыл важнейшую общую теорему, но был также и активным участником полевых геодезических измерений. П. Л. Чебышевым была сформулирована теорема о «наивыгоднейшей» (в некотором смысле) проекции, которая даёт практические рекомендации картографам.
Казалось бы, окончательное наилучшее решение задачи уже должно быть найдено. Но на самом деле невозможно создать карту точную, сохраняющую все расстояния, поэтому на любой плоской карте есть искажения. Это следует из теоремы Гаусса, названной им самим «замечательной»: при отображении, сохраняющем расстояния, одной поверхности на другую будут совпадать их гауссовы кривизны в соответствующих точках. Гауссова кривизна — это числовая характеристика, которая даёт представление о степени и характере искривлённости поверхности в данной точке. И поскольку у глобуса (сферы) кривизна всюду положительна, а у плоскости — нулевая, отобразить сферу на плоскость с сохранением расстояний не удастся. С другой стороны, можно доказать, что поверхность нулевой кривизны можно «развернуть» на плоскость с сохранением расстояний.
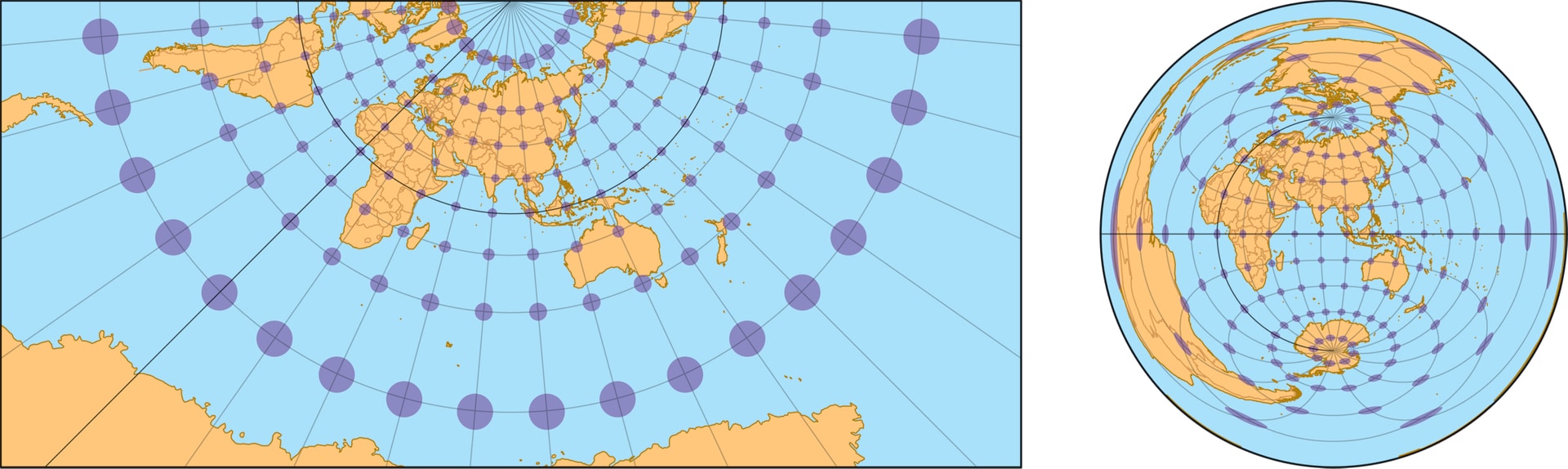
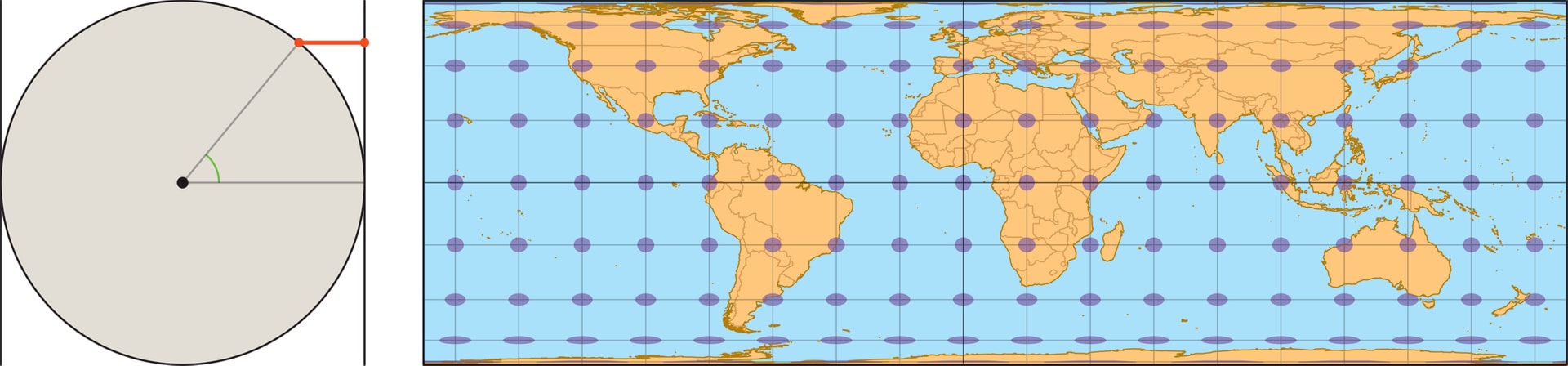
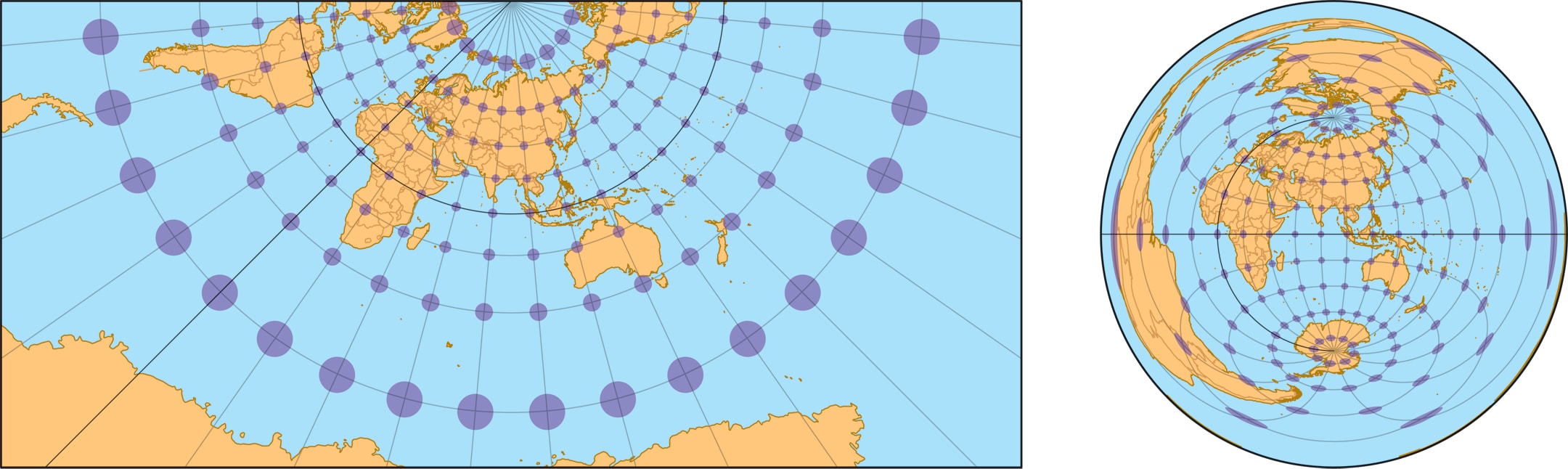
Причина появления искажений в том, что при любой проекции (отображении) сферы на плоскость расстояния между точками изменяются неодинаково. Степень растяжения или сжатия длин путей может зависеть и от положения точки на глобусе, из которой выходят пути, и даже от направления их выхода из точки. Визуальное представление об искажениях можно получить, рассматривая на карте образы одинаковых маленьких окружностей на глобусе. Эти образы, называемые эллипсами искажений, демонстрируют зависимость изменений в равноудалённости точек окружностей от их центров, то, как эти изменения выглядят по разным направлениям.
Но если искажения всюду и разные, то что означает масштаб, всегда указываемый на карте? Все привыкли думать, что это единый коэффициент изменения размеров изображений объектов на карте в сравнении с размерами самих объектов на поверхности Земли. На самом деле на карте приводится так называемый главный масштаб — отношение размеров картографируемого глобуса и Земли. Это оправданно, поскольку проекция глобуса на карту всегда выбирается так, чтобы были точки или линии без искажений. Но необходимо добавить и предостережение: для других линий масштаб отличается от главного и вычисление реальной длины пути по измерениям на карте не сводится к умножению на главный масштаб.
Для использования карт в практических задачах желательно, чтобы какие‐то характеристики (свойства) на глобусе сохранялись при отображении на карту. По этому принципу среди картографических проекций выделяют три основных типа: равновеликие, равнопромежуточные, равноугольные.
Равновеликая проекция при отображении на карту сохраняет площади всех областей. Следовательно, отношение площадей участков земной поверхности сохраняется не только на глобусе, но и на карте. Заметный недостаток проекции — значительное искажение на общей карте Земли контуров крупных областей (например, континентов). Карты данного типа применяются как для решения задач в масштабах Земли, когда надо сравнивать площади больших территорий и целых стран, так и в делах, требующих подробных карт, планов, — в сельском хозяйстве, геологоразведке.
Равнопромежуточность подразумевает сохранение каких-либо длин. Часто используемый вариант — сохранение длин (главного масштаба) на меридианах. Искажения углов (контуров областей) на таких картах меньше, чем при равновеликой проекции. Карты в равнопромежуточной проекции привычны, «хорошо читаются».
Равноугольная проекция в любой точке сохраняет углы между путями, выходящими из неё. Из этого условия можно вывести, что масштаб в точке для всех направлений одинаков (образы окружностей на сфере — окружности на карте) и зависит только от положения точки. Карты с равноугольной проекцией стали незаменимыми спутниками в путешествиях, на суше и на море.
Например, в спортивном ориентировании удобно работать с картами в равноугольной проекции. Во‐первых, равноугольность позволяет точно идти по азимуту, во‐вторых, на такой карте маленькие территории изображаются почти без искажений их формы, что позволяет узнавать детали местности.
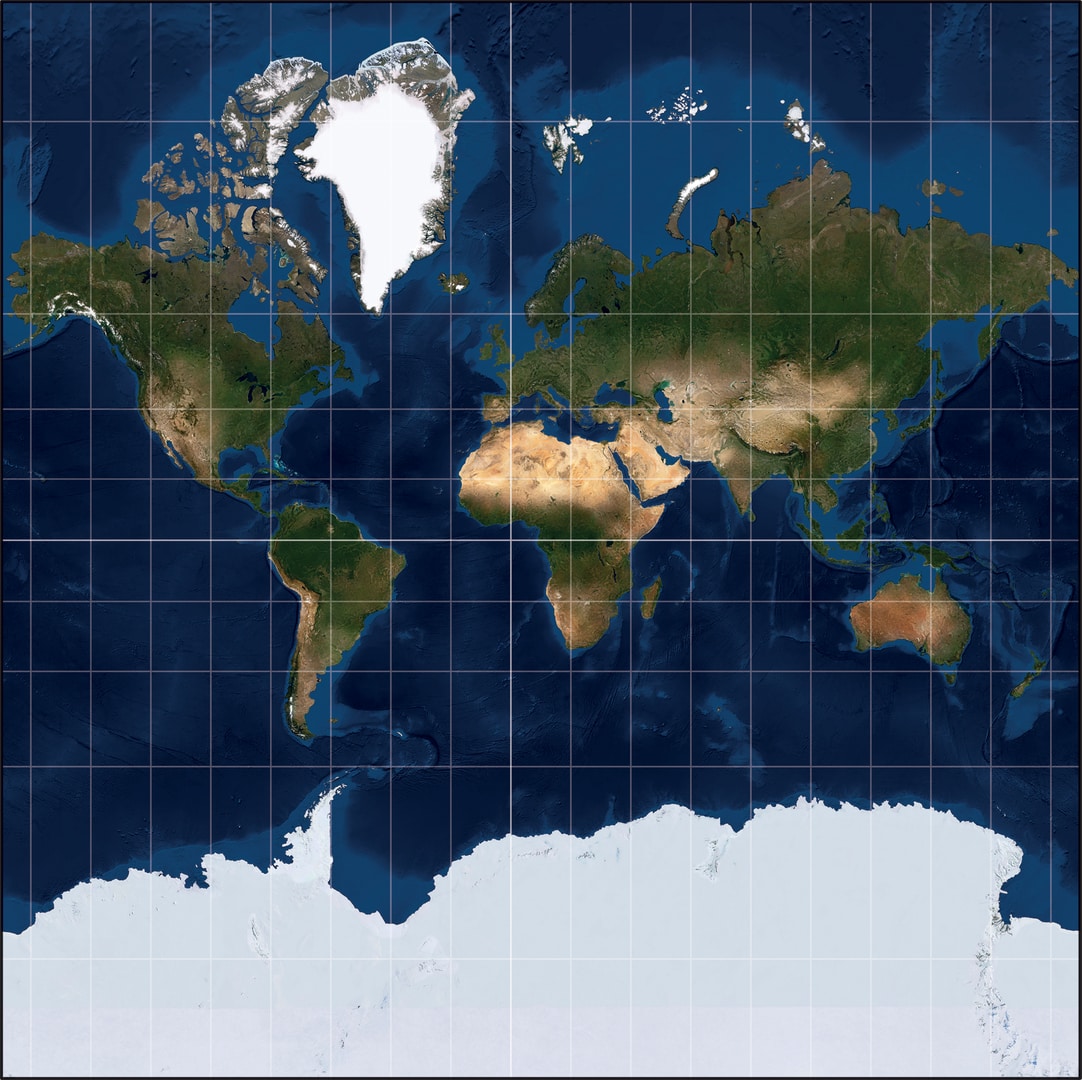
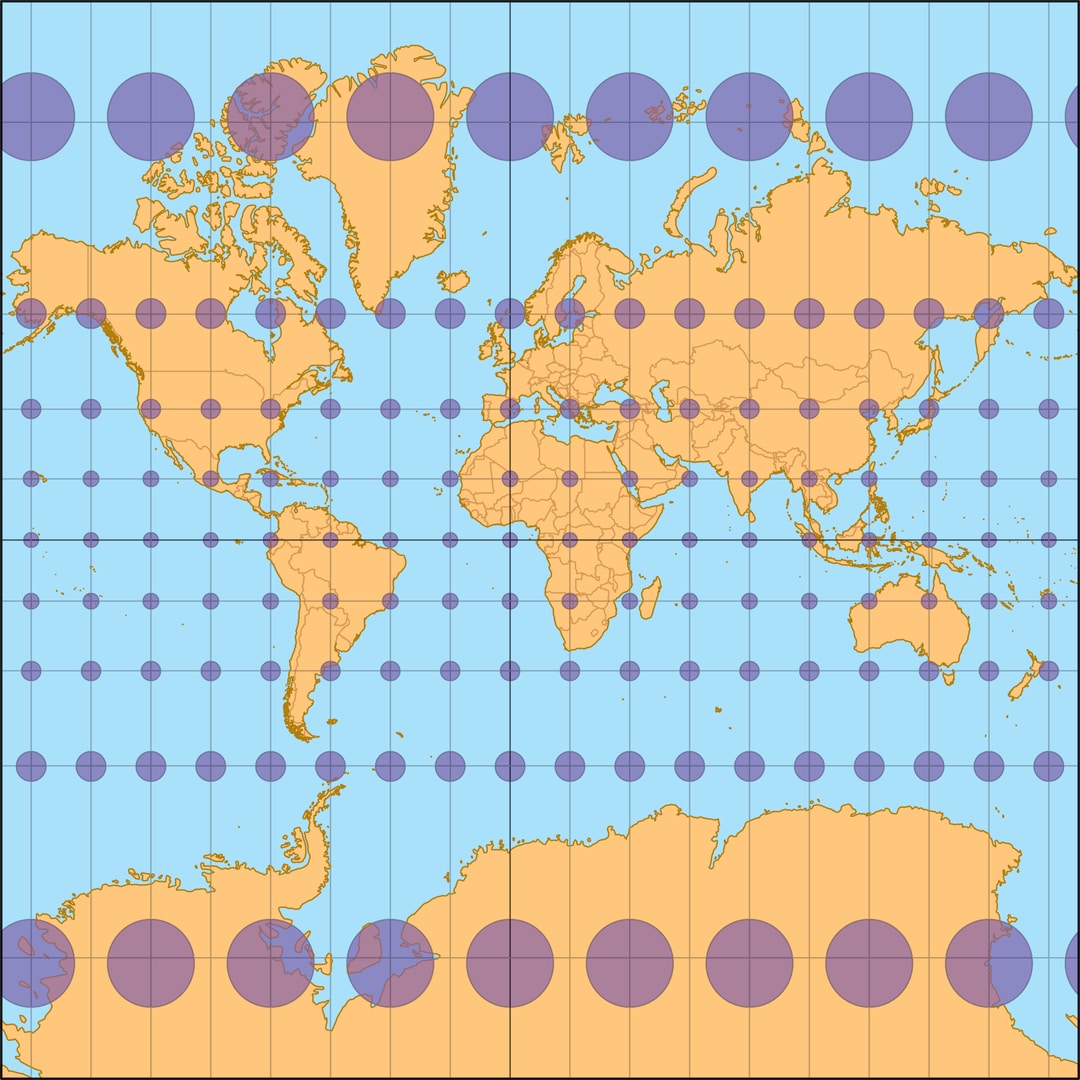
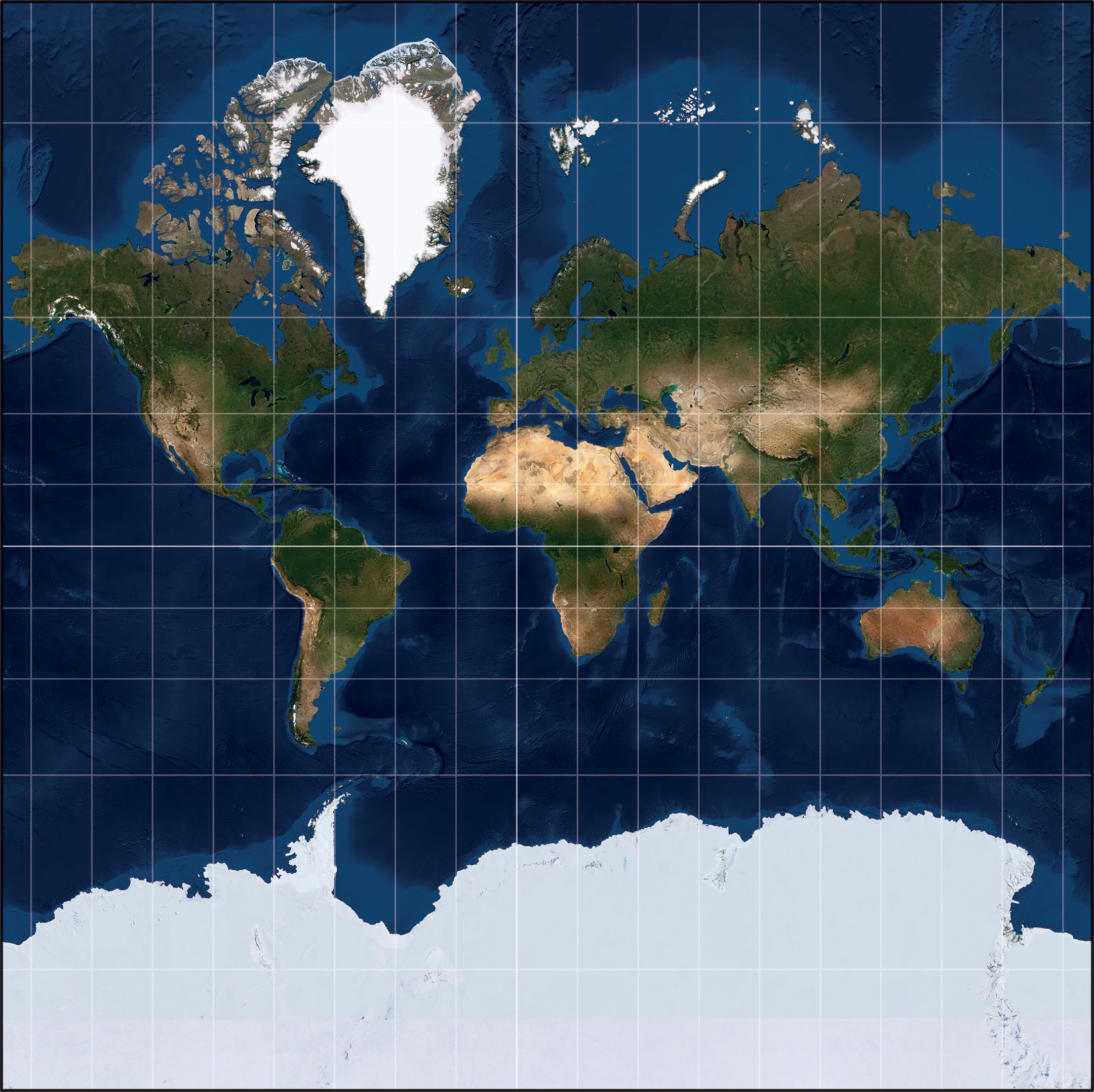
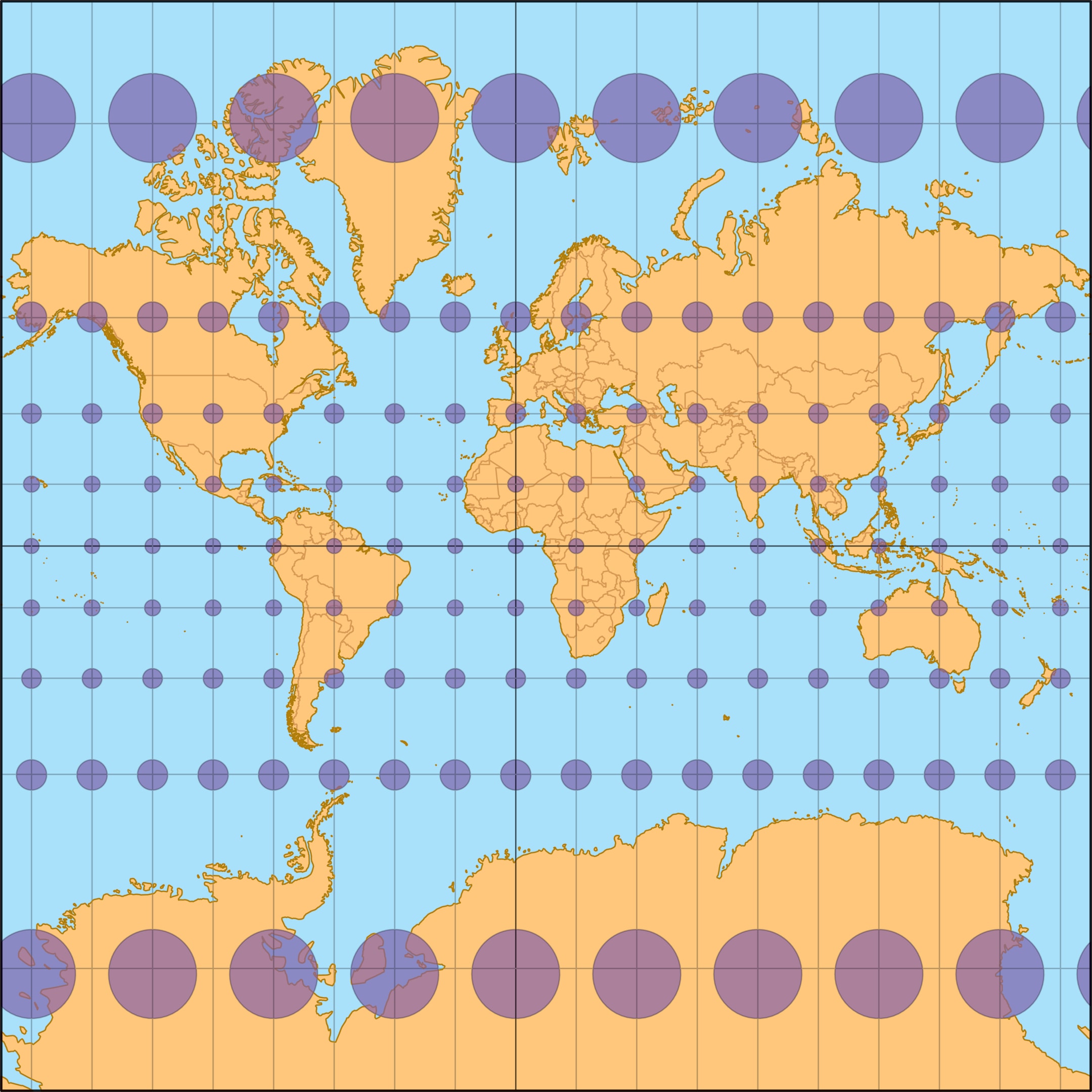
При плавании в открытом море, напротив, видимых ориентиров нет. Более четырёх веков главной морской картографической проекцией является равноугольная проекция Меркатора (1569 год). На такой карте меридианы и параллели представлены вертикальными и горизонтальными (взаимно перпендикулярными) прямыми.
Чтобы решить задачу прокладывания курса корабля, можно просто соединить на карте два пункта отрезком и определить угол пересечения прямой с меридианами. Вследствие равноугольности проекции Меркатора под тем же углом будет пересекать меридианы Земли маршрут, определяемый данной прямой. Полученный маршрут постоянного путевого угла — не наикратчайший, но управление кораблём будет простым и понятным: держать постоянный курс.
Проекция Меркатора служит основой также «сухопутных» топографических карт в ряде стран Европы и Америки. Она же — основа самых распространённых электронных карт, установленных на каждом смартфоне, и программ в навигаторах.
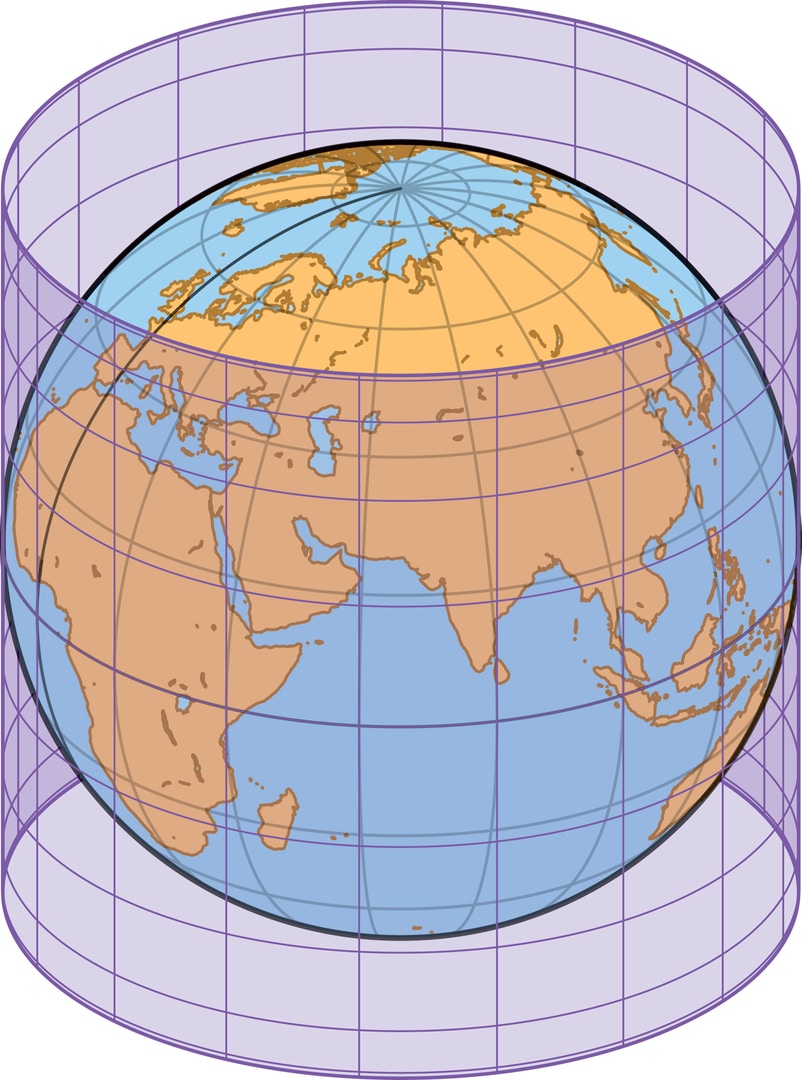
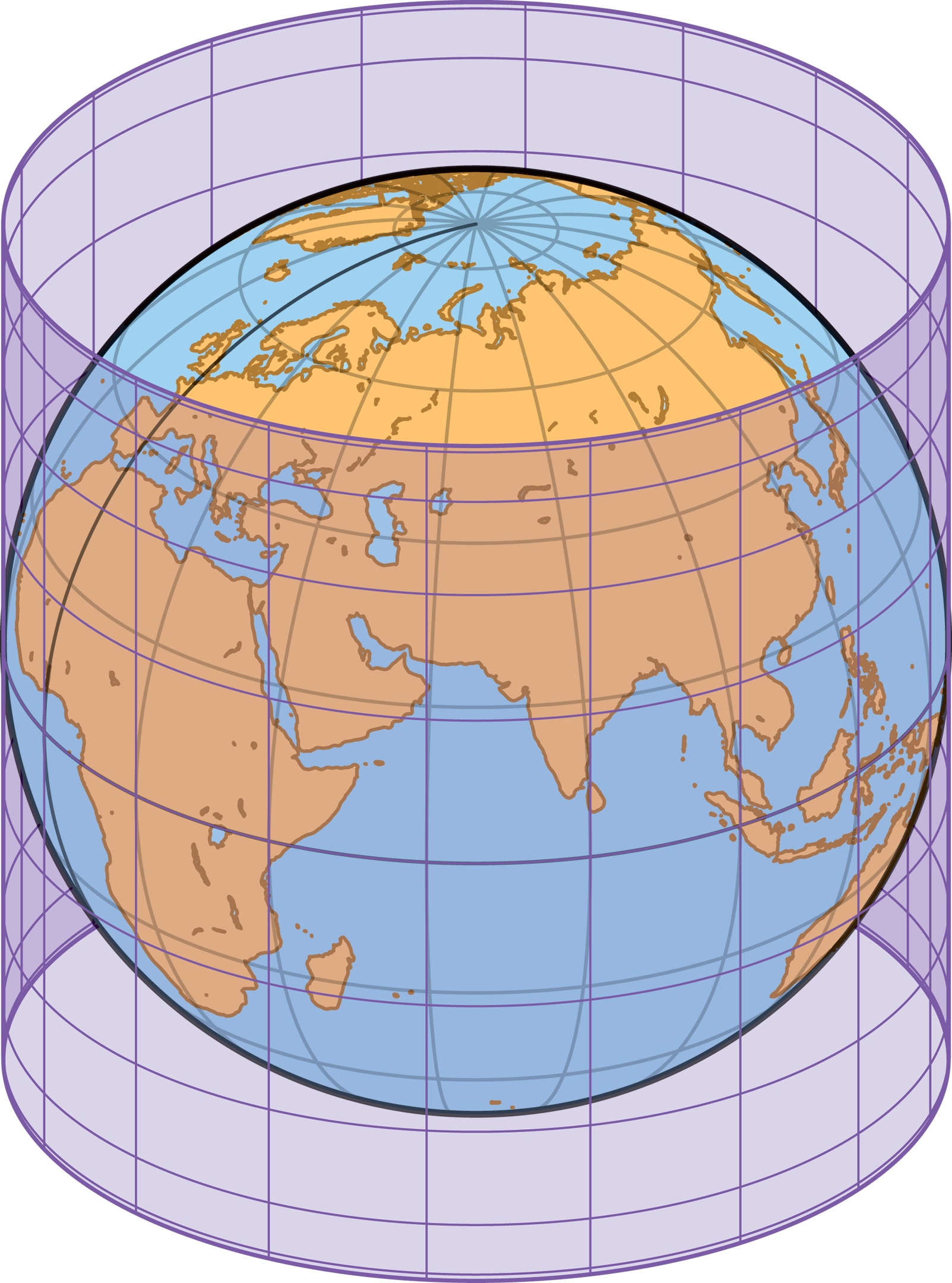
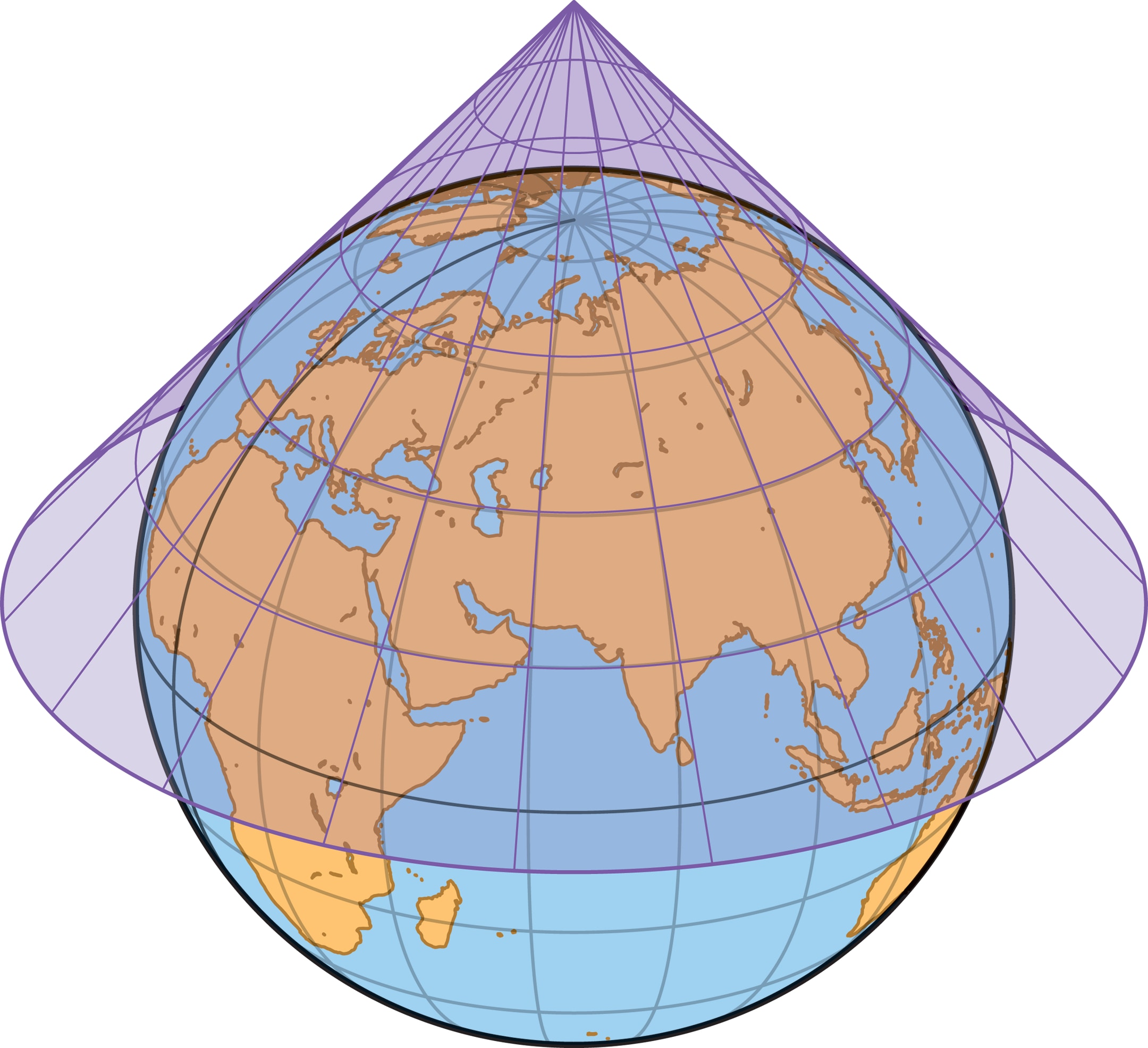
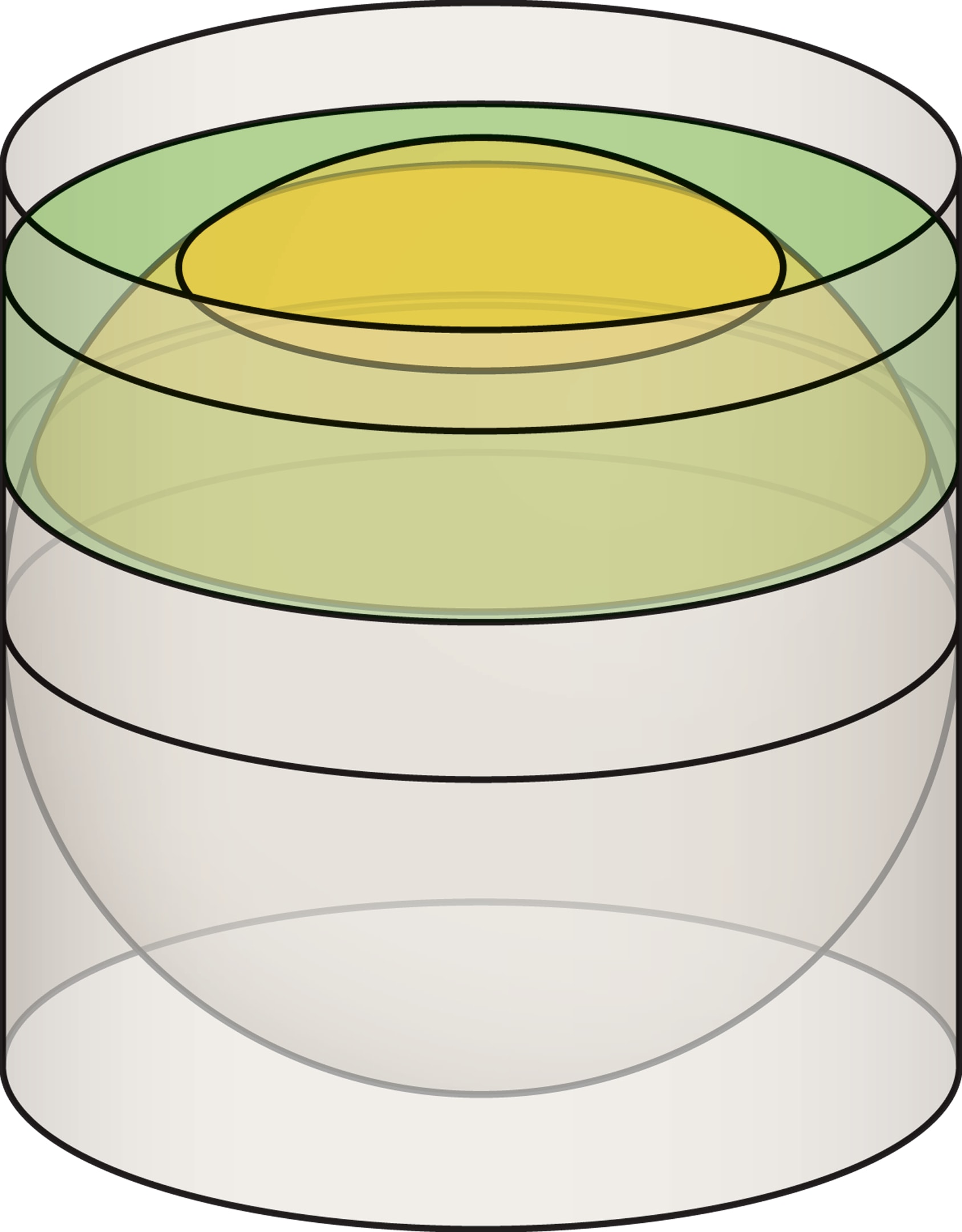
Построить картографическую проекцию с заданными свойствами геометрически возможно разными способами. Среди самых распространённых вариантов два «подсказывает» упоминавшаяся теорема Гаусса — это цилиндрическая и коническая проекции. На первом шаге сфера отображается на развёртывающуюся поверхность (нулевой кривизны) — цилиндр или конус. А затем эту поверхность с полученным изображением «разворачивают» на плоскость, уже без искажений. Самый наглядный вариант, можно сказать, классический — когда ось цилиндра (или конуса) совпадает с осью Земли.
Если цилиндр касается глобуса, то экватор — их общая линия — при проекции «остаётся на месте», поэтому масштаб вдоль экватора не меняется. Более того, касание поверхностей означает их сходство в малой окрестности точки касания, поэтому неудивительно, что и искажения длин при переходе со сферы на цилиндр оказываются весьма небольшими в узкой полоске вдоль экватора.
Можно выбрать и цилиндр, радиус которого меньше, чем у глобуса. Пересечением сферы и цилиндра будут две окружности, масштаб будет сохраняться вдоль обеих параллелей. В частности, это можно использовать при картографировании территорий, расположенных и к северу, и к югу от экватора. Но и для территории в одном полушарии такая проекция представляет интерес: можно обеспечить отсутствие искажений в точках важной для страны параллели.
При естественном проецировании глобуса на цилиндр меридианы переходят в вертикальные прямые, параллели — в окружности. При разворачивании цилиндра окружности-параллели переходят в прямые, и сетка меридианов и параллелей на глобусе превращается в прямоугольную сетку на карте-прямоугольнике.
Если цилиндр касается глобуса, то декартова координата $x$ пропорциональна долготе: $x\sim \lambda$. Масштаб на каждой параллели будет постоянным, но различным на разных параллелях (поскольку на глобусе они имеют разную длину). А вот с декартовой координатой $y$ однозначности нет: картинку на цилиндре можно растягивать по вертикали, причём коэффициент растяжения может зависеть от широты точки.
Например, можно выбрать растяжение так, что проекция окажется равнопромежуточной (на меридианах). Достаточно в качестве второй декартовой координаты взять широту: $y\sim\varphi$. Геометрически: ниточку, натянутую от экватора до полюса по меридиану, распрямляют на цилиндр. Эту проекцию придумал древнегреческий картограф Марин Тирский (II век н. э.). В современном мире она используется во многих геоинформационных системах.
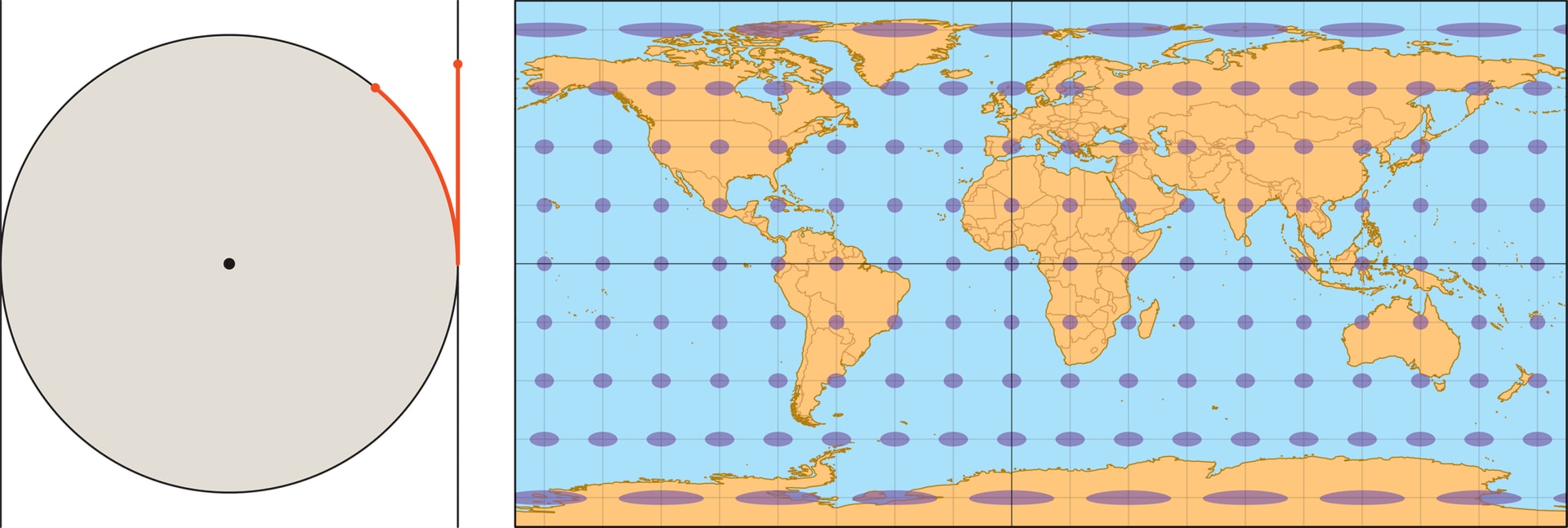
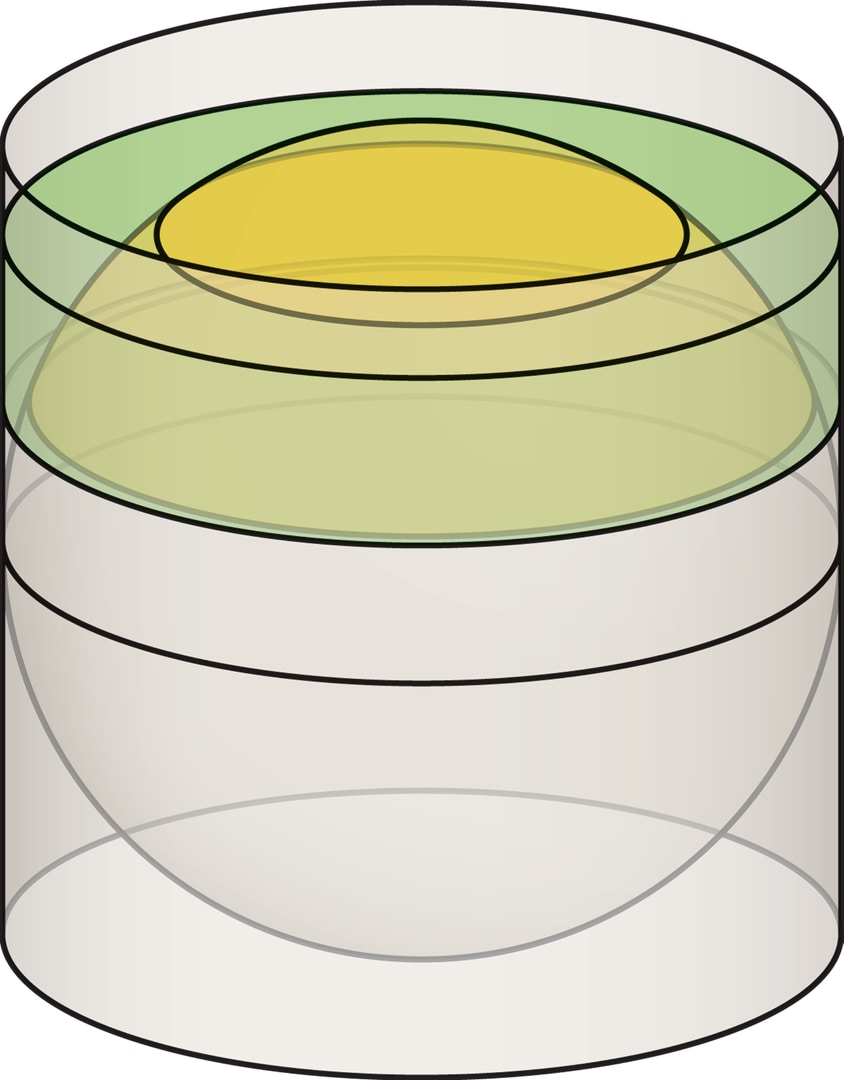
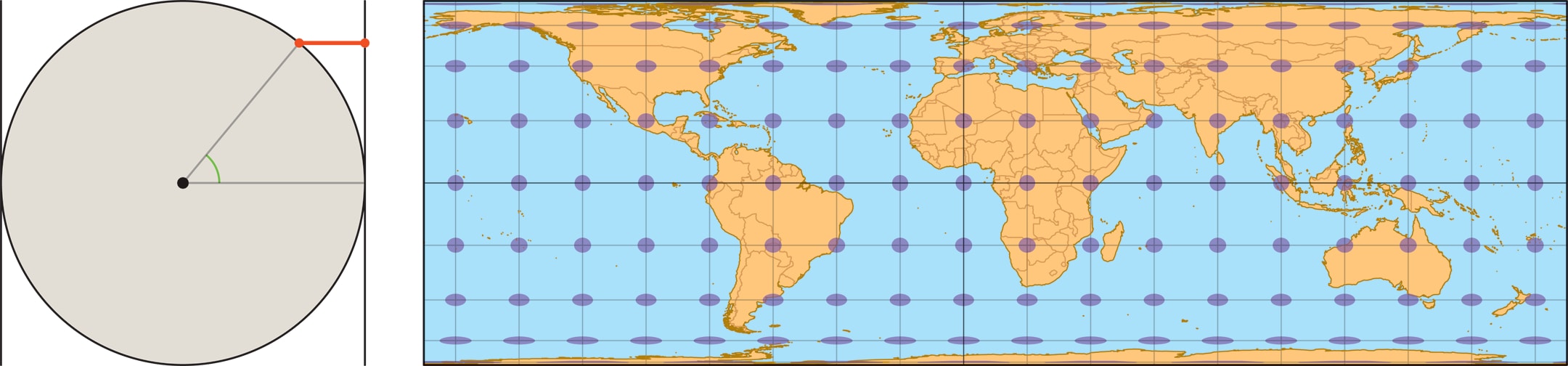
Равновеликую цилиндрическую проекцию разработал в 1772 году математик и астроном Иоганн Ламберт. (Кстати, он же чуть раньше доказал, что знаменитое число $π$ — иррациональное.) В этой проекции $y\sim\sin\varphi$, т. е. проецирование дуги меридиана на цилиндр происходит горизонтально, «по определению» синуса. Равновеликость вытекает из того, что площадь полосы между двумя параллелями на глобусе равна площади её горизонтальной проекции на цилиндр.
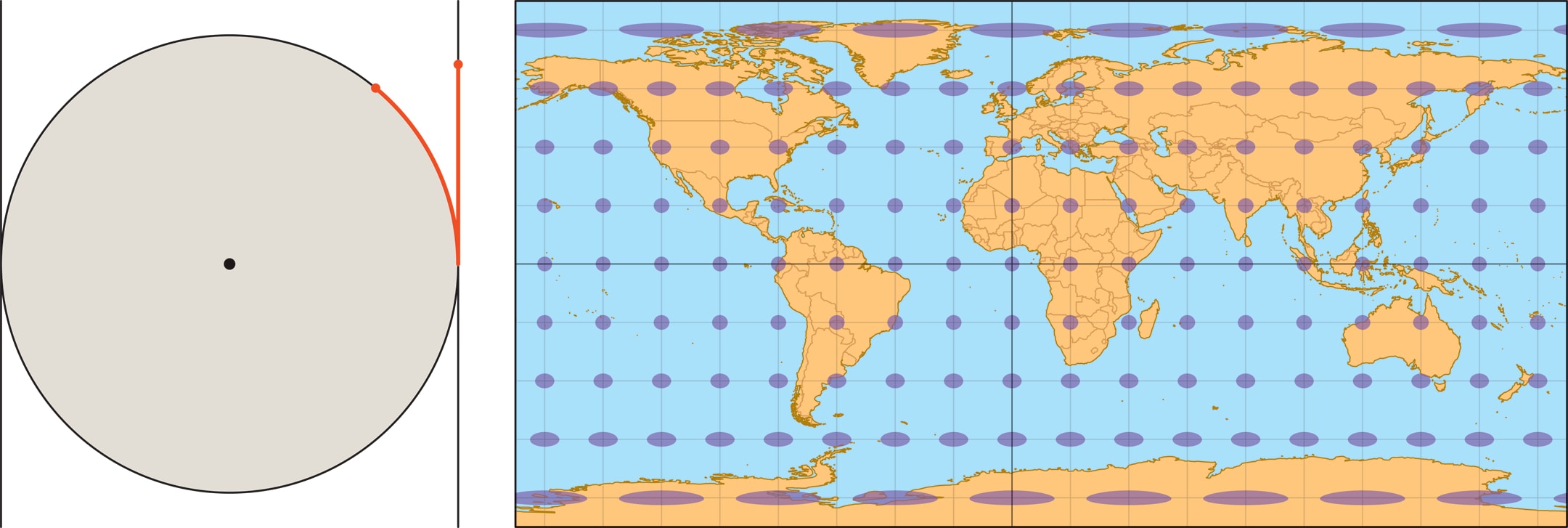
Можно построить и равноугольную проекцию, если вспомнить про связь равноугольности с независимостью масштаба в точках от выбора направлений выходящих путей. Надо выбрать растяжение так, чтобы в каждой точке масштаб вдоль параллели совпадал с масштабом вдоль меридиана. Масштаб вдоль параллели определяется тем, что проекция цилиндрическая, он увеличивается при движении от экватора к полюсу. Поэтому и расстояния между горизонтальными образами параллелей стандартной сетки на глобусе увеличиваются с ростом широты. В результате получается уже знакомая проекция Меркатора, в которой $y\sim\ln \tg \bigl(\frac{\varphi}{2}+\frac{π}{4}\bigr)$. При приближении точки на глобусе к полюсам значение этой функции «уходит в бесконечность», поэтому образы полюсов физически не могут появиться на такой карте, и обычно её укорачивают, не изображая на ней полярные шапочки.
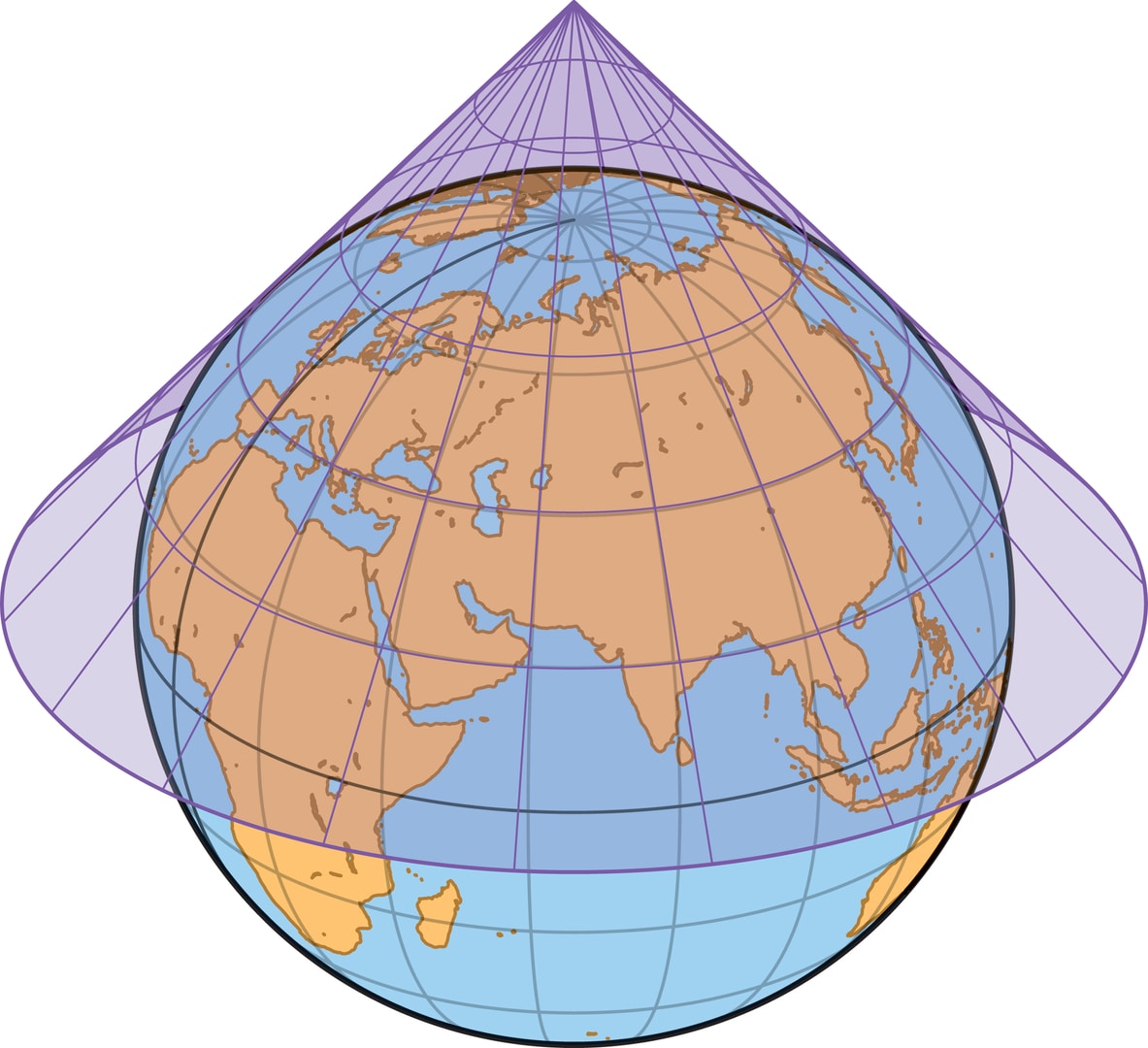
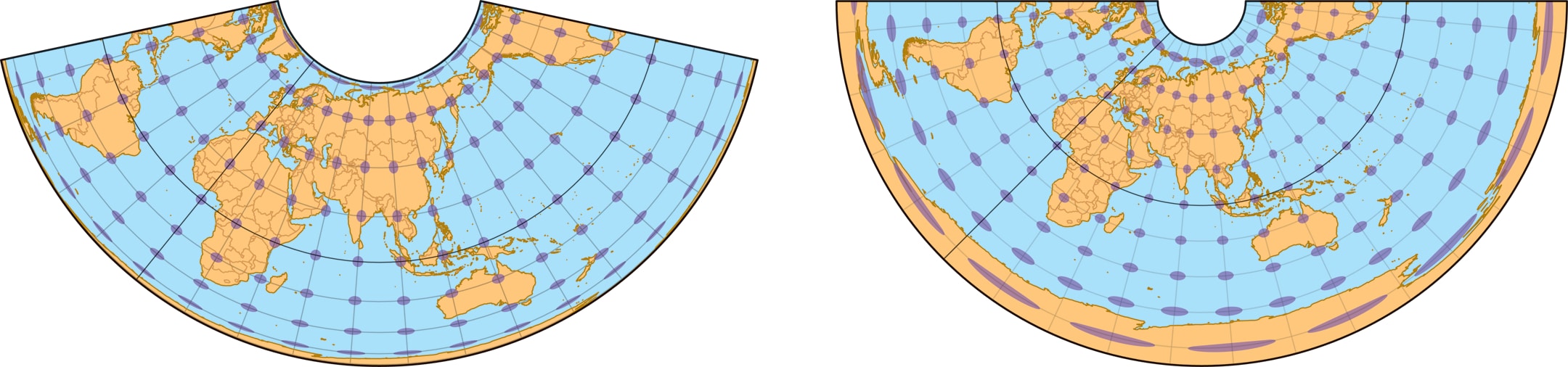
Конические проекции похожи на цилиндрические — и по построению, и по свойствам. В конической проекции, как и в цилиндрической, меридианы переходят в прямые на плоской карте, но параллели теперь превращаются в дуги окружностей, при этом линии разных семейств, как и раньше, пересекаются под прямыми углами.
Но у конуса в сравнении с цилиндром больше настроек: можно выбирать и положение вершины на оси глобуса, и угол раствора. Например, можно выбрать параметры конуса так, что он будет касаться поверхности глобуса по выбранной параллели на территории картографируемой страны. Как и в случае касания глобуса с цилиндром, в точках параллели масштаб сохранится, а в полосе, окружающей параллель, искажения будут незначительными.
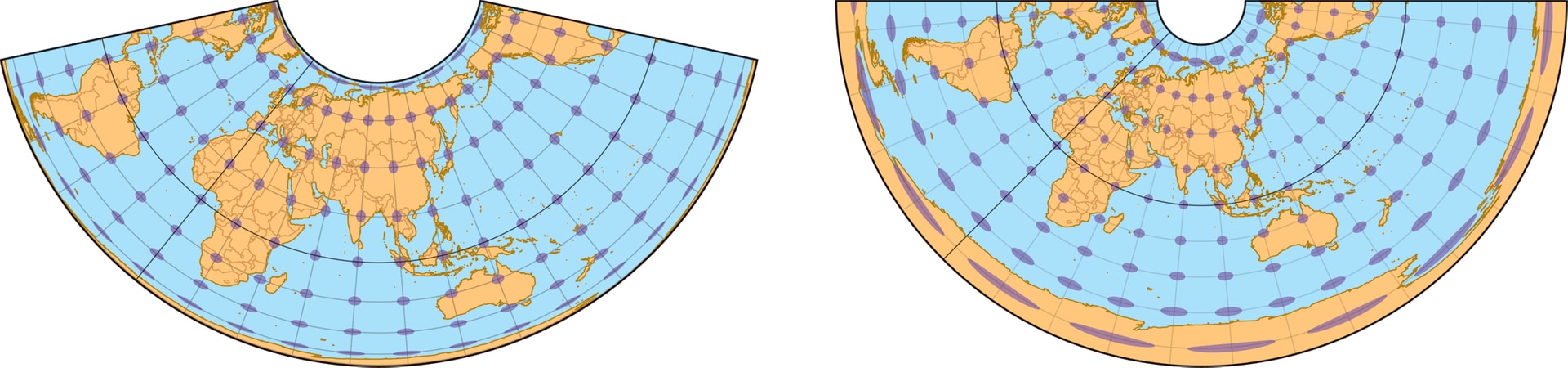
Пересечение конусом глобуса по двум окружностям, близким к северной и южной границам страны, сохраняет масштабы на окружностях и позволяет надеяться, что и в полосе между ними (т. е. на всей территории страны) искажения будут не очень значительными. Оба варианта «настройки» конической проекции особенно актуальны при картографировании стран, протяжённых по долготе — например, России.
В конической проекции (подобно цилиндрической) растяжением вдоль образующих конуса можно добиться, чтобы проекция стала равновеликой, равнопромежуточной или равноугольной. В российской картографии среди конических проекций равнопромежуточные чаще применяют для создания карт всей страны, а равноугольные используются для картографирования отдельных областей.
Координатные сетки цилиндрической или конической проекции в классическом варианте (когда ось совпадает с осью глобуса) можно узнать сразу. В первом случае сетка прямоугольная, во втором — состоит из прямых и дуг окружностей. Ещё одна классическая координатная сетка состоит из концентрических окружностей и их радиусов. Окружности — образы параллелей на глобусе, радиусы — меридианов. Так выглядят карты в азимутальной полярной проекции, их форма соответствует сетке — круглая. «Изготовление» классической азимутальной сетки можно представить так: вырежем из резинового глобуса шапочку вокруг полюса и прижмём её к плоскости, чтобы она «расплющилась». Переход параллелей в окружности и меридианов в отрезки порождает соответствующие преобразования угловых координат на глобусе в полярные координаты на карте: широта становится характеристикой удалённости окружности от центра (радиус), долгота переходит в полярный угол.
Тип этой сетки не изменится, если растягивать картинку вдоль радиусов (коэффициент растяжения в точке, т. е. степень «расплющивания» резиновой шапочки, зависит от расстояния до центра и не зависит от направления). Свобода действий позволяет создавать азимутальные проекции с требуемыми свойствами.
Азимутальная равновеликая проекция (И. Ламберт): глобус лежит на плоскости карты; хорда, соединяющая точку касания с точкой на глобусе, «шарнирно» опускается в плоскости меридиана на карту, определяя проекцию точки.
А на эмблеме Организации Объединённых Наций представлена азимутальная полярная равнопромежуточная проекция (не меняются расстояния вдоль меридианов).
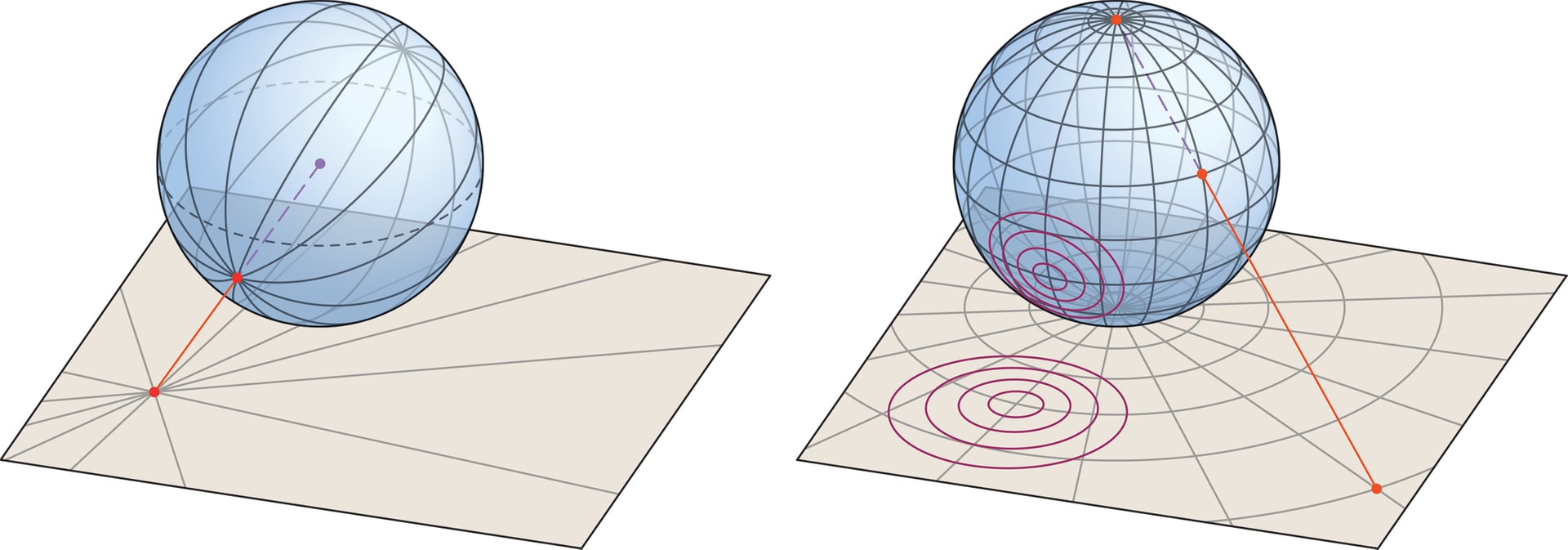
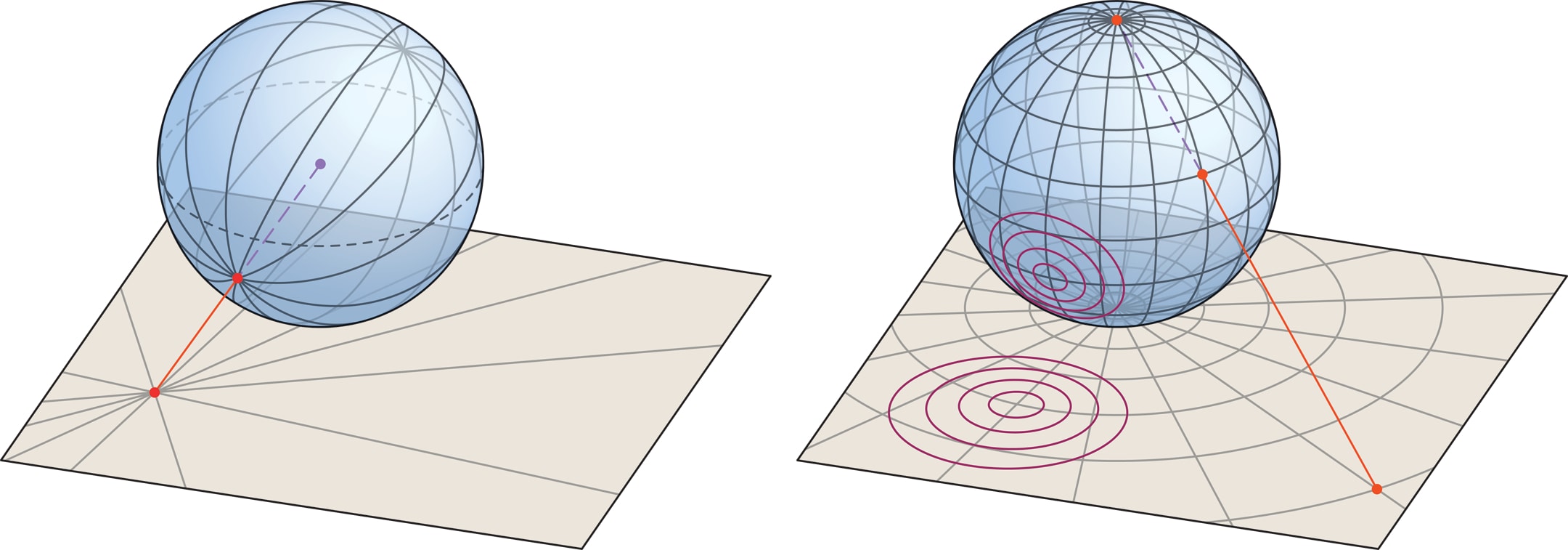
Целая группа азимутальных проекций получается с помощью центрального проецирования. Полярный вариант — когда плоскость карты касается глобуса в одном из полюсов, а центр проекции находится на оси Земли: вне Земли — внешняя азимутальная проекция, на поверхности (в полюсе) — стереографическая, в центре Земли — гномоническая. Азимутальная проекция точки на глобусе — пересечение с плоскостью карты луча, проведённого из центра проекции через данную точку. В зависимости от расположения центра меняются и свойства проекции, и её возможные применения.
Внешняя проекция — взгляд из космоса со спутника на обращённое к нему полушарие Земли.
Стереографическая проекция — самая «умная», она сохраняет все углы (т. е. является равноугольной) и в дополнение сохраняет один, но важный тип кривых —окружности. Точнее, окружности, не проходящие через полюс, переходят в окружности на плоскости, а проходящие через него (не только меридианы!) — в прямые. Эта проекция представляет на карте всю поверхность Земли, исключая полюс — центр проекции.
Если центр проекции находится в центре Земли, то дуга любого большого круга переходит в прямую. Это означает, что кратчайший путь между точками поверхности Земли изображается на карте отрезком прямой, становится «видимым». И хотя проекция не сохраняет расстояния, углы и площади, она оказывается полезным инструментом.
Все описанные картографические проекции были представлены в классических полярных вариантах — их ось совпадала с осью глобуса. Но для создания карт специального назначения можно перевести ось проекции и на другой земной диаметр. С одной стороны, привычные координатные сетки при косой проекции могут измениться до неузнаваемости, с другой — карта становится ещё более гибким инструментом. Например, подобную идею реализуют в авиационных и сейсмических картах, где расстояние от фиксированного центра до любой точки должно быть наглядным и легко измеряемым. Удобный вариант — азимутальная равнопромежуточная карта, центром которой служит центр событий.
Рассмотренная классификация картографических проекций, основанная на способе проецирования (цилиндрические, конические, азимутальные) и на типе искажений (равновеликие, равнопромежуточные, равноугольные), не является полной.
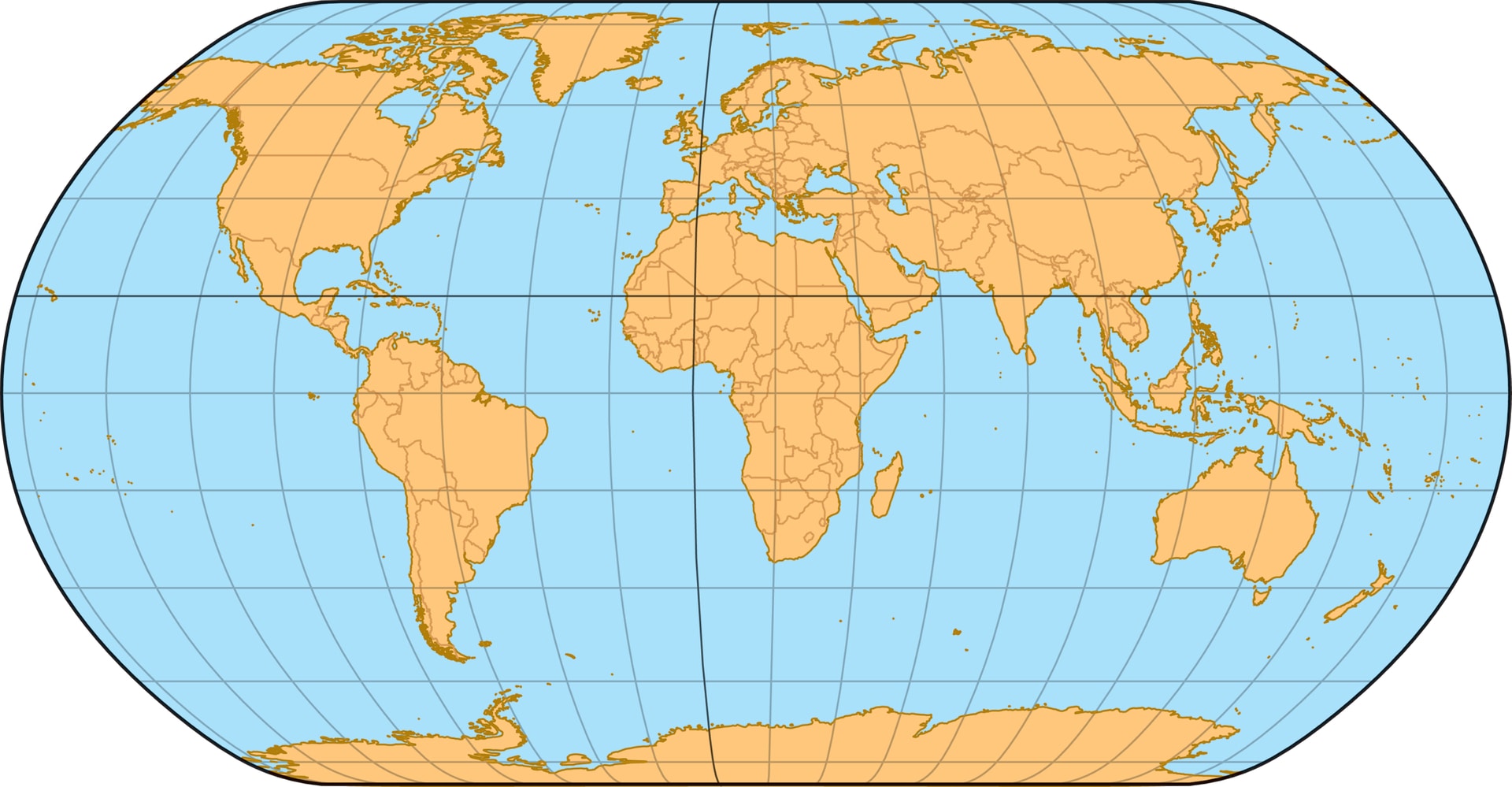
Читатель может встретить проекции, координатные сетки которых лишь напоминают одну из классических. В названиях таких проекций отражают и то, на что они похожи, и то, что они «ненастоящие». Например, есть общие карты Земли, на которых параллели — прямые, а меридианы при приближении к полюсам изгибаются в сторону Гринвичского меридиана. Такая сетка напоминает классическую прямоугольную, и проекцию называют псевдоцилиндрической.
Интересные и полезные проекции можно получить, если условия сохранения свойств сделать менее категоричными, точными, жёсткими. В частности, речь может идти о создании «гармоничной» проекции, в которой всё хорошо в среднем: минимизируется суммарное искажение углов, площадей и т. д. Задача отыскания такой проекции была поставлена П. Л. Чебышевым, и им же была сформулирована теорема, ставшая в картографии рабочим инструментом: среди равноугольных проекций области земной поверхности наилучшей является та, у которой масштаб вдоль границы — величина постоянная.
До сих пор рассказ о картографических проекциях носил описательно-наглядный характер. В математической картографии уже давно чисто геометрические подходы заменены аналитическими, формульными. Задачи, условия, требования, которым должна соответствовать создаваемая карта, превращаются в уравнения, связывающие координаты точек на глобусе и на карте. На этом языке может быть представлено всё: от желания получить прямоугольную сетку до равноугольности будущей проекции. Причём в уравнениях можно отразить не только «упрощённый» сферический глобус, но и более близкий к реальности глобус-эллипсоид. Уравнения сложные, их изучение и решение всегда требовало не только упорства и изобретательности, но и использования «новейших» математических достижений. Ещё в проекции Меркатора появились тангенсы и диковинные для того времени логарифмы; стереографическая проекция тесно связана с изучением комплексных чисел. И в наши дни с применением разнообразных математических инструментов разрабатываются новые картографические проекции. Но теперь они служат не только штурманам и путешественникам, а всем, кто выбирает маршрут в современном мире.
Равноугольные проекции в каждой точке сохраняют углы между проходящими через неё путями и масштаб по всем направлениям. А для страны, изображение которой на глобусе является односвязной областью (т. е. граница состоит из одного «куска», является связной кривой), такая проекция приобретает дополнительные настройки. Знаменитую теорему Бернхарда Римана из комплексного анализа о конформных (сохраняющих углы) отображениях можно перефразировать на картографическом языке: для любой «односвязной» страны можно подобрать равноугольную проекцию так, что плоская карта страны будет кругом, а её столица — центром этого круга.
Для интересующихся теорией функций комплексного переменного приведём полную формулировку теоремы Римана. Для любой односвязной области $G$ в расширенной комплексной плоскости $\overline{\mathbb C}$, граница которой содержит более одной точки, найдётся конформное отображение области $G$ на единичный круг $B_1(0)= \{w\colon |w|<1\}$. Такое отображение будет единственным, если выбрать произвольные $z_0\in G$, $w_0\in B_1(0)$, $α\in [0, 2π)$ и задать условия нормировки: $f(z_0)=w_0$, $\arg f'(z_0)=α$.
При рассмотрении равновеликой цилиндрической проекции было отмечено, что площадь сферической полосы, вырезаемой двумя параллельными плоскостями, равна площади соответствующей цилиндрической полосы. Это приводит к интересному наблюдению: площадь полосы на глобусе зависит только от расстояния между секущими плоскостями, но не зависит от близости полосы к экватору или полюсу. «Съедобное» толкование: если круглый неочищенный апельсин нарезать на ломтики одинаковой толщины, то и площадь шкурки у всех кусков будет одинакова.
Понятие кривизны встречается в нескольких сюжетах книги, геометрический взгляд на это понятие — тема статьи «Искривлённые миры».
Слово «карта» — ядро термина «картография». Оно пришло из латыни (carta), а туда попало из Греции как название бумаги из папируса. Географические карты в немецком, русском, французском — от этого корня. А в английском, испанском, итальянском — это, соответственно, map, mapa, mappa (слова тоже родом из латыни, где mappa — ткань, салфетка; в латынь это слово пришло из финикийского языка). Расхождение названий связано с материалом, который использовали в разных странах при изготовлении карт — бумага или ткань. Любопытно, что игральные карты во всех этих странах делали из бумаги (card, karte, carte и т. д.).
Познакомиться с результатами великих математиков в области картографии можно по изданным на русском языке сборникам их работ: Леонард Эйлер «Избранные картографические статьи» (М.: Изд‐во геодезической литературы, 1959); Карл Фридрих Гаусс «Избранные геодезические сочинения» (М.: Изд‐во геодезической литературы, 1957, 1958); Пафнутий Львович Чебышев «Полное собрание сочинений» (Т. 5: Прочие сочинения. Биографические материалы. М.: Изд‐во АН СССР, 1951).
Березин В. Н., Смолянский М. Л. Портреты Земли
Маркушевич А. И. Комплексные числа и конформные отображения. — 2‐е изд. — М.: ГИФМЛ, 1960. — (Популярные лекции по математике; Вып. 13). — [Стр. 29—31].
Куприн А. М. Слово о карте. — М.: Недра, 1987.
Географический атлас для учителей средней школы. — 4‐е изд. — М.: ГУГК, 1985.
Багров Л. История русской картографии. — М.: Центрполиграф, 2005.
Бугаевский Л. М. Математическая картография: Учебник для вузов. — М.: Златоуст, 1998.
Берлянт А. М. и др. Картоведение: учебник для вузов. — М.: Аспект Пресс, 2003. — (Классический университетский учебник).