Простейшая (но исторически заслуженная!) механическая конструкция, позволяющая нарисовать достаточно сложную кривую, такова: в заданных точках штырьками фиксируется положение гибкой и упругой пластины, определяющее гладкую линию.
Самым распространённым устройством во времена «ручного» рисования чертежей было лекало — плоская линейка, границы которой были готовым набором разнообразных гладких кривых.
Затем настало время использования кривых, заданных формулами. В наши дни результаты использования гладких «формульных» кривых видит на экране монитора каждый компьютерный пользователь. А самым распространённым инструментом для создателей компьютерной графики являются кривые Безье — элемент всех графических программ и систем автоматизированного проектирования.
Работа этого инструмента основана на результатах математических исследований, восходящих к XIX веку.
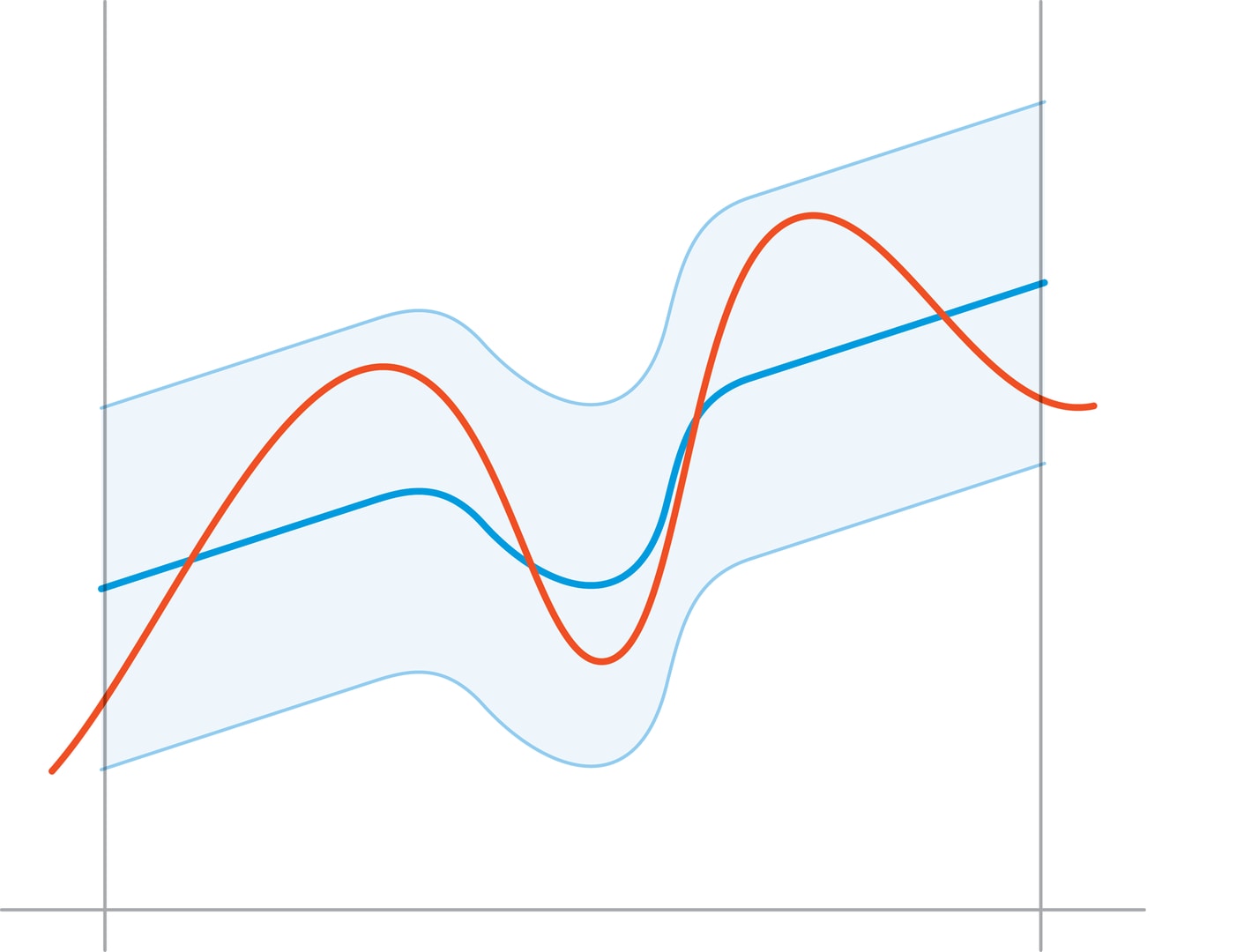
В 1885 году немецкий математик Карл Вейерштрасс доказал, что любую непрерывную на отрезке функцию можно с любой точностью приблизить алгебраическими многочленами (функциями вида $a_nx^n+a_{n-1}x^{n-1}+…+a_2x^2+a_1x+a_0$). Геометрически теорему Вейерштрасса можно пояснить так. Если вы провели над отрезком кривую линию, перемещая карандаш слева направо и не отрывая его от листа бумаги (т. е. изобразили график непрерывной функции), то для произвольно узкой полоски, окружающей кривую, найдётся многочлен, график которого проходит внутри этой полоски.
В чём ценность этой теоремы для нематематиков? Если необходимо нарисовать плавную линию, например, создавая логотип, контур автомобиля или букву шрифта, то можно ограничиться графиками многочленов, поскольку любую гладкую кривую можно заменить графиком многочлена так, что эти две линии на глаз будут неразличимы. При этом способ представления кривой будет простым и удобным, в том числе для компьютера. Вместо задания линии значениями в точках (а для представления гладкой кривой точек должно быть очень много) необходимо задать лишь небольшой набор чисел — коэффициенты многочлена. При поточечном задании линии ни о каком векторном формате речь идти не может — после увеличения масштаба картинки точки будут разрежены, а в случае задания многочленом возможность масштабирования обеспечивается автоматически.
Ввиду большой значимости теоремы Вейерштрасса для развития самой математики стали появляться различные варианты её доказательства. Однако когда в 1912 году появилось полуторастраничное доказательство российского математика С. Н. Бернштейна, оно произвело огромное впечатление неожиданностью подхода и красотой. Это доказательство было конструктивным — в явном виде предъявлялся многочлен, удовлетворяющий условиям теоремы. Впоследствии эти многочлены назвали многочленами Бернштейна.
На практике гладкую кривую приходится собирать из частей. И в этой работе более гибким инструментом, по сравнению с многочленами, являются сплайны. Если отрезок разбит на несколько более мелких отрезков и определённые на них алгебраические многочлены (полиномы) можно в точках разбиения «гладко склеить», то получится сплайн (кусочно-полиномиальная функция).
Упоминавшиеся кривые Безье, используемые в компьютерной графике, — это сплайны, в конструкции которых полиномы Бернштейна выступают как «строительные кирпичики». Впервые кривые Безье появились в 60‐х годах XX века, когда П. Безье и П. де Кастельжо независимо разработали методы проектирования кузовов автомобилей, основанные на применении сплайнов.
Разумеется, представлена только одна линия в удивительнойи одновременно типичной для математики эволюции теоремы Вейерштрасса: от изначально чисто теоретического утверждения до конкретных практических приложений.
Например, квадратичные кривые Безье — составленные из многочленов второго порядка — используются в формате компьютерной анимации SWF. Кубические кривые Безье используются в PostScript, PDF, SVG и других графических программах и форматах. Использовались они и при создании этой книги — как иллюстраций, так и шрифта, которым напечатан текст.