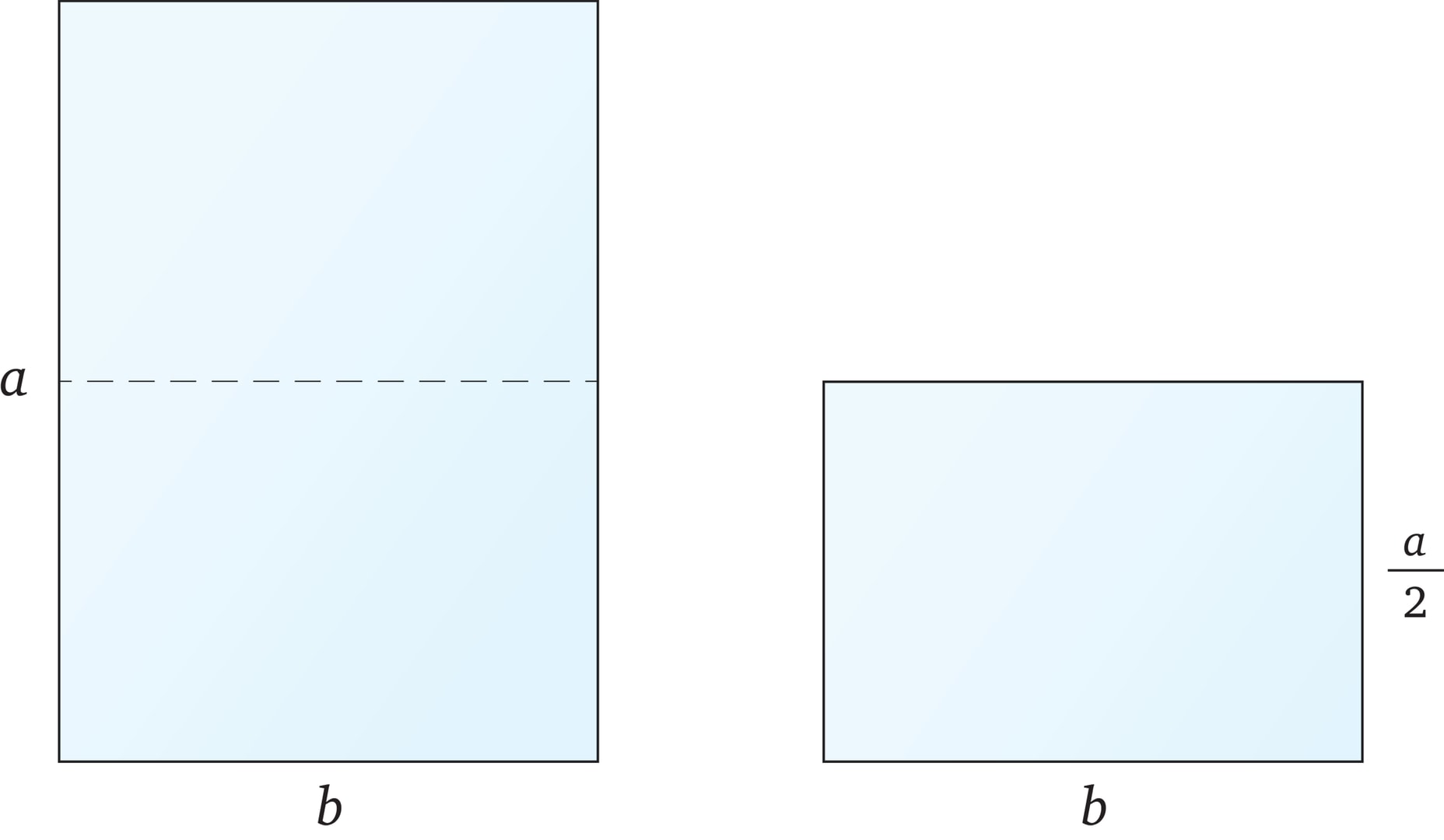
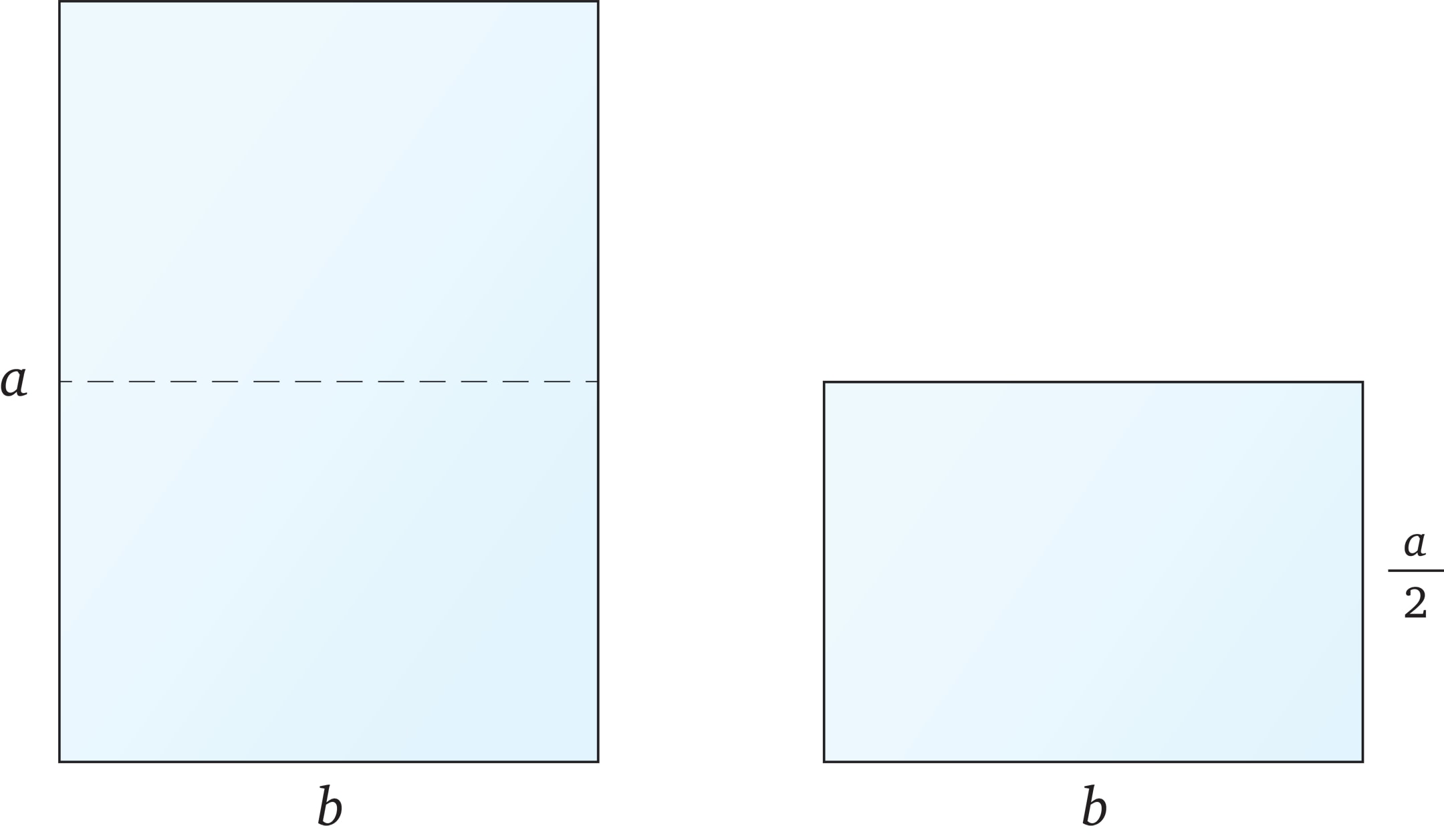
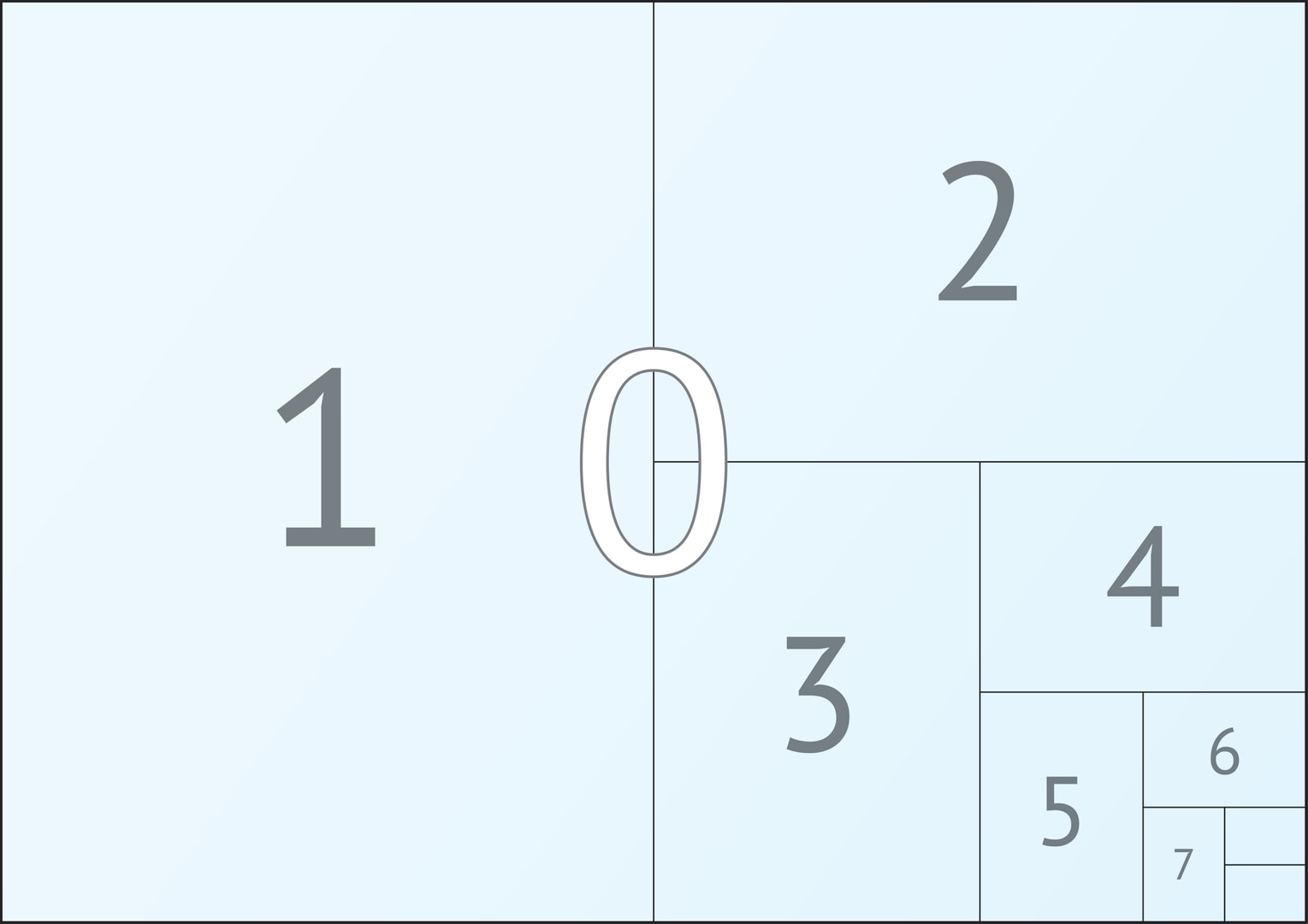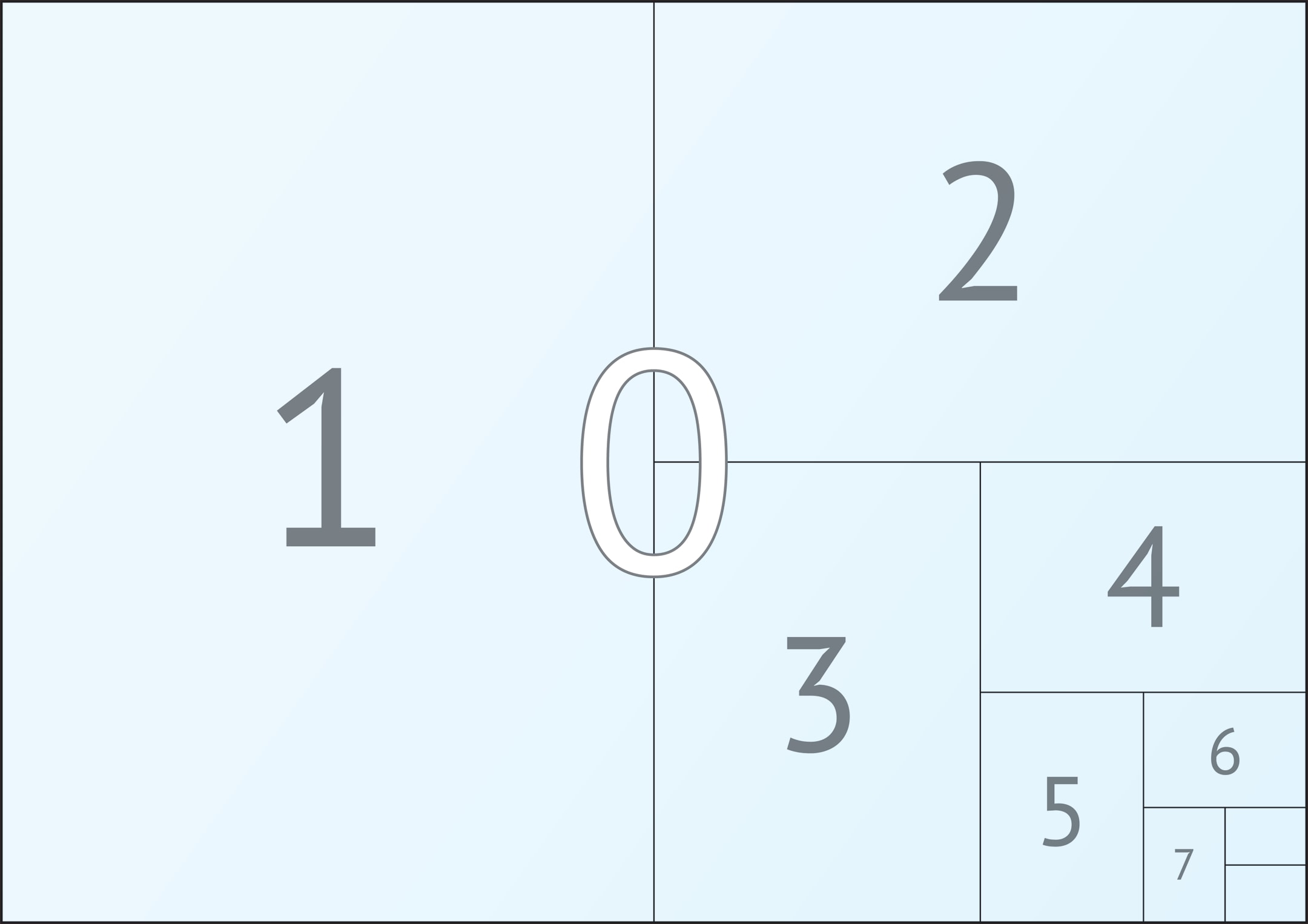Каким должно быть отношение сторон прямоугольного листа бумаги, чтобы у половины этого листа было такое же отношение сторон?
Представим сформулированное условие в виде формулы: $$ \frac{a}{b}=\frac{b}{a/2}. $$
Отсюда находим отношение сторон: $$ \frac{a}{b}=\sqrt{2}.$$
У листа с таким отношением сторон имеется свойство, ценное и в делопроизводстве, и в полиграфии: сложив его пополам, мы получим лист с теми же пропорциями и, значит, также удовлетворяющий сформулированному требованию. С точки зрения геометрии, всё дело в том, что исходный прямоугольник и его половина подобны. А если листы подобны, то макет страницы, разработанный для одного из них, можно перенести на второй простым масштабированием.
Стандарты на бумажные форматы, удовлетворяющие сформулированному требованию, были введены в 20‐х годах XX века. Применяются серии «А», «B», «С», каждая состоит из последовательности уменьшающихся листов. Выбор самого большого листа в серии («базового», получающего нулевой индекс), связан с той или иной нормировкой. В каждой серии лист с номером $n+1$ выглядит как сложенный вдвое лист с номером $n$.
Число $\sqrt{2}$, которое теоретически определяет отношение сторон прямоугольных листов всех номеров во всех сериях, является иррациональным. Это означает, что число $\sqrt{2}$ нельзя представить в виде отношения двух целых чисел, соответствующая ему десятичная дробь — бесконечная непериодическая $$ \sqrt{2}=1,414213562373…$$
На практике приходится использовать рациональные числа. В выборе форматов серий «А», «B», «С» длины сторон листов выражаются целыми числами (в миллиметрах), эти числа подобраны так, чтобы их отношение было близким к $\sqrt{2}$.
В серии «А» в качестве листа А0 взят лист, имеющий размеры $1189\times 841$ мм. Размеры листа выбраны так, что его площадь (с большой точностью) равна одному квадратному метру. В повседневной жизни наиболее часто встречается формат бумаги A4. Длины сторон листа равны 297 и 210 мм, это примерно одна четвёртая часть длин сторон листа A0, площадь листа A4 — примерно 1/16 квадратного метра. При плотности стандартной офисной бумаги 80 грамм на квадратный метр, один лист весит около 5 грамм, а пачка из 500 листов — $2,5$ килограмма.
В серии «B» лист B0 выбран так, что длина его меньшей стороны равна 1 метру. Чтобы отношение сторон было близко к $\sqrt{2}$, в качестве большей стороны листа принято значение $1,414$ м. Область применения серии «B» — специальные разделы делопроизводства. Например, паспорт гражданина Российской Федерации имеет формат B7 — $125\times 88$ мм, что соответствует рекомендациям, содержащимся в международном стандарте.
Знание отношения сторон в формате А и десятичной записи числа $\sqrt{2}$ облегчает выполнение стандартных офисных операций. Например, как на копировальном аппарате перевести лист А4 в лист А3? Коэффициент подобия этих листов равен $\sqrt{2}$, для решения задачи копирования можно взять приближённое значение $\sqrt{2}≈ 1{,}4$ и выставить на ксероксе коэффициент увеличения, равный 140%. А если надо «превратить» лист А4 в лист A5, то коэффициент уменьшения будет равен $\frac{1}{\sqrt{2}}$. Замечательно, что его «рабочее» значение легко найти и без технических средств: $\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2}≈ 0{,}7$. Значит, на ксероксе нужно выставить показатель 70%.
Среди форматов серий «A», «B» и «C» первый — самый «правильный» с точки зрения приближения ключевого числа $\sqrt{2}$ рациональными дробями.
Цепная дробь (см. статью «Високосное летосчисление», и список литературы к сюжету) числа $\sqrt{2}$ бесконечна, её элементы — двойки: $$ \sqrt{2}=1+ \frac1{2+\frac1{2+\frac1{2+\frac1{2+\frac1{2+\vphantom{\frac12} \dotsm }}}}}. $$
Приведём первые подходящие дроби разложения: $$ \displaylines{ 1,\quad 1+\frac{1}{2}=\frac{3}{2},\quad 1+\frac1{2+\frac1{2}}=\frac{7}{5},\quad 1+\frac1{2+\frac1{2+\frac1{2}}}=\frac{17}{12},\cr 1+\frac1{2+\frac1{2+\frac1{2+\frac1{2}}}}=\frac{41}{29},\quad 1+\frac1{2+\frac1{2+\frac1{2+\frac1{2+\frac1{2}}}}}=\frac{99}{70}.\cr} $$
Значение $\frac{41}{29}=1{,}41379…$ — неплохое рациональное приближение числа $\sqrt{2}=1{,}41421…$, оно фактически определяет базовый лист А0: его размеры $1189\times 841$ мм соответствуют пропорции $\frac{41}{29}=\frac{1189}{841}$.
Производные размеры листов серии «A» получаются последовательно делением большей стороны пополам: $841\times 594$ мм (А1), $594\times 420$ мм (А2), $420\times 297$ мм (А3), $297\times 210$ мм (А4). Видно, что «основой» форматов А2 и А4 является лучшее приближение числа $\sqrt{2}$, чем у А0: $\frac{99}{70}=\frac{594}{420}=\frac{297}{210}$, дробь $\frac{99}{70}=1{,}41428…$ отличается от $\sqrt{2}$ только в пятом знаке после запятой в десятичном разложении.
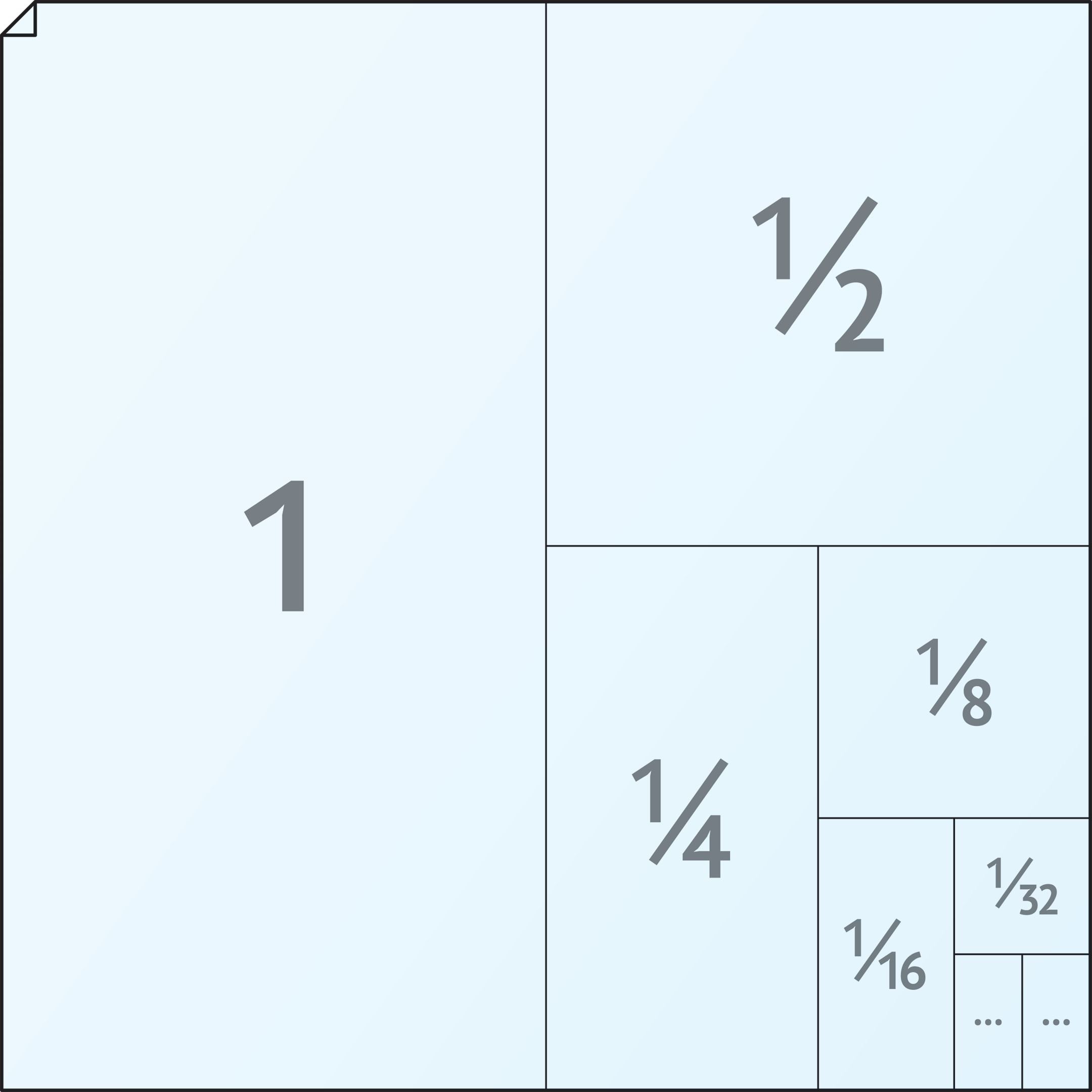
Рисунок, на котором были представлены форматы, можно использовать и для геометрической иллюстрации того, почему сумма бесконечной геометрической прогрессии (см. «Практическая бесконечность») $$ 1+\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+\frac{1}{2^4}+\frac{1}{2^5}+… $$ равна 2. Пропорции листа в этом случае роли не играют.